Unleash the dino: Time-based strategies to improve password cracking
Looking to improve your skills? Discover our trainings sessions! Learn more.
Problem definition
Sample performance
The Kraqominus rig
- Kraqozorus software
- 1 GPU RTX 2080Ti
- 1 CPU i7-4730K
- JohnTheRipper Jumbo
- Hashcat 6.1.1
Sample cracking times
| Hash function | Estimated time | Mean Speed Hashcat | Mean Speed JohnTheRipper |
|---|---|---|---|
| Bcrypt | 694287.9 y | 300 H/s | 250 H/s |
| Sha512crypt | 770.0 y | 270 KH/s | 4 KH/s |
| Sha1 | 4.4 d | 15 GH/s | 30 MH/s |
| MD5 | 23.3 h | 79 GH/s | 50 MH/s |
| NT | 23.2 h | 79.5 GH/s | 65 MH/s |
- run tailored attacks, using knowledge acquired during the engagement
- run as many attacks as possible in the alloted time
Strategies
- Simplify the cracking process
- Save time
- Increase the percentage of cracked passwords
- Brute-force
- Wordlists
- Wordlists + rules
- Wordlists combination
- Wordlists + masks
- Masklists
- Recycling cracked passwords
- Single mode
As a reminder, a rule-based attack consists of a bunch of mutations (modify, cut, extend, duplicate, ... ) on a given wordlist and a mask-based attack represents a subset of a brute-force attack, it's more specific, so by definition, faster.
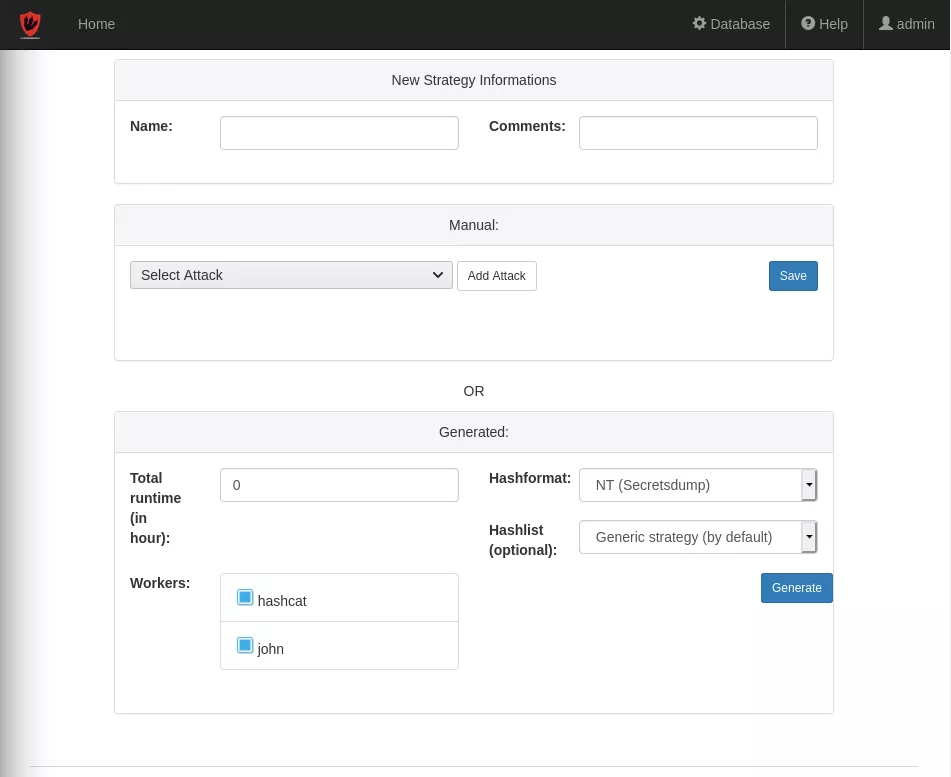
Manual strategy
Brute-force strategy:
- full 1 to 7
- lower, digits, upper 8-length words
- lower, digits 9-length words
Wordlists strategy:
- 4 wordlists (~106 GB): breachcompilation, hashes.org (2012 to mi-2020), probv2-huge and internal-all (custom-wordlist)
Mixed strategy:
- single mode with rules: single and jumbo
- wordlists: m3g9tr0n, crackstation, entr0py, rockyou, probv2-huge, internal-all
- wordlists with rules: m3g9tr0n+hob064, crackstation+hob064, entr0py+hob064, rockyou+hob064, rockyou+10000randrules, internal-medium+internal-prior, breachcompialtion+dive
- brute-force: 3 to 7
- masks: lower*6+digit*2, lower/upper*1+lower*4+digit*3, upper*1+lower*3+digit*4
Generated strategy
- genetic optimization approach
- "black box" solver approach
- Select all potential attacks, and compute statistics regarding their efficiency (this is called an Item)
- Identify overlaps between attacks
- Run the optimizer, using the list of Items and the information on overlapping attacks
User interface
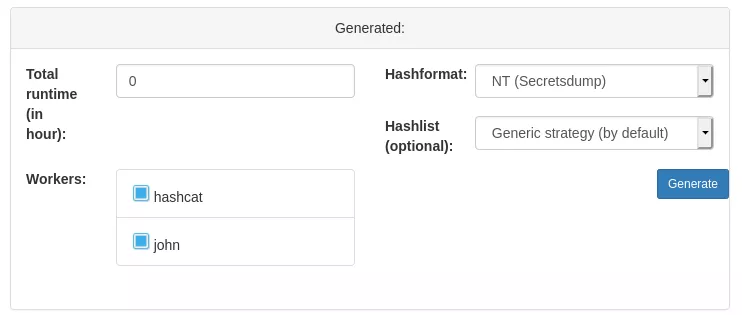
- allotted time, which is the maximum amount of time the attack is allowed to run
- the hash format, in order for the optimizer to evaluate how much time each attack will take
- the workers, they are the cracking units that form your cracking cluster
Potential attacks selection
- the total amount of cracked password
- if the hashformat is unsalted, the mean duration of this attack
- it the hashformat is salted, it will use the ETA (estimated time) computed by the ratio between the keyspace size and the cracking speed. If the attack time is greater than the time bound, it will be rejected outright
- the attack name
- the total amount of passwords cracked by this attack
- the average duration of this attack, using the specified hash format
Attack overlap detection
- To resolve this problem for masks, Kraqozorus computes the intersections between each pair of masks. If this intersection is not empty, a bilateral incompatibility between them is created in the dictionary.
- To create incompatibilities for wordlists, we use the label of a wordlist attack. By convention, it is structured as <name_wordlist>-<size_or_date> (for example, rockyou-small or custom_wordlist-2020). We then use the hypothesis that rockyou-large overlaps with rockyou-small, but not with custom_wordlist-2020.
- In the case of rules based attacks, the wordlist overlap check is combined with a check based on the name of the rule.
- In the case of wordlists + masks attacks, the wordlist overlap check is combined with the mask overlap check.
Below a snippet of code which shows a standalone tool to compute overlapping between masks.
#!/usr/bin/env python3
from typing import Tuple, Dict, List, Set, Optional
from json import loads
import functools
CHARSET_l = set(range(ord('a'), ord('z') + 1)) # lower
CHARSET_u = set(range(ord('A'), ord('Z') + 1)) # upper
CHARSET_d = set(range(ord('0'), ord('9') + 1)) # digits
CHARSET_h = CHARSET_d | CHARSET_l # lower hex
CHARSET_H = CHARSET_d | CHARSET_u # upper hex
CHARSET_s = {ord(x) for x in " !\"#$%&'()*+,-./:;<=>?@[\\]^_`{|}~"} # special
CHARSET_a = CHARSET_l | CHARSET_u | CHARSET_d | CHARSET_s # all
CHARSET_b = set(range(0, 256)) # bits
CHARSETS = {
'l': CHARSET_l,
'u': CHARSET_u,
'd': CHARSET_d,
'h': CHARSET_h,
'H': CHARSET_H,
's': CHARSET_s,
'a': CHARSET_a,
'b': CHARSET_b,
'?': {ord('?')}
}
class ItemMask:
''' Class to store mask's properties '''
def __init__(self, mask, custom_charset=()):
self.mask = mask
self.custom_charset = custom_charset
def _expand_mask(
mask: str,
custom_charsets: Tuple[Optional[str], Optional[str], Optional[str], Optional[str]],
) -> List[Set[int]]:
''' Expand the mask to obtain all the solution space '''
out: List[Set[int]] = []
i = 0
while i < len(mask):
cur = mask[i]
if cur == '?' and i + 1 < len(mask):
i += 1
typ = mask[i]
if typ in ('1', '2', '3', '4'):
out.append(_expand_custom_charset(custom_charsets[int(typ) - 1]))
else:
out.append(CHARSETS.get(typ, set()))
else:
out.append({ord(cur)})
i += 1
return out
def _expand_custom_charset(
cs: Optional[str]
) -> Set[int]:
''' expand the solution space of the mask depending on the custom charsets (?1,?2,?3,?4) '''
if not cs:
return set()
out = set()
i = 0
while i < len(cs):
cur = cs[i]
if cur == '?' and i + 1 < len(cs):
i += 1
out |= CHARSETS.get(cs[i], set())
else:
out.add(ord(cur))
i += 1
return out
def _mask_overlap(
mask1: List[Set[int]],
mask2: List[Set[int]]
) -> Tuple[int, int]:
''' check if a collision exists between 2 masks '''
card = functools.reduce(
lambda acc, n: acc * len(n),
mask1,
1)
# masks do not have the same length, can't overlap
if len(mask1) != len(mask2):
return (card, 0)
common = 1
for (c1, c2) in zip(mask1, mask2):
common *= len(c1 & c2)
if common == 0:
break
return (card - common, common)
def get_incompatibilities_mask_type(
items: List[ItemMask]
) -> Dict[int, List[int]]:
''' get the incompatibilities dictionnary for the attack type involving a mask '''
incompatibilities_mask: Dict[str, List[str]] = {k.mask: [] for k in items}
for maskattack in items:
incompatibilities_mask[maskattack.mask] = []
# list of all maskattacks minus the selected maskattack
potential_incompatibilities = items.copy()
potential_incompatibilities.remove(maskattack)
mask_expansion = _expand_mask(maskattack.mask, maskattack.custom_charset)
for candidate in potential_incompatibilities:
candidate_mask_expansion = _expand_mask(candidate.mask, candidate.custom_charset)
_, common_mask = _mask_overlap(mask_expansion, candidate_mask_expansion)
if common_mask != 0:
incompatibilities_mask[maskattack.mask].append(candidate.mask)
return incompatibilities_mask
def file_to_items(filein):
''' Create a list of ItemMask from the content of the json file '''
items = []
filein_content = {}
with open(filein, 'r') as fin:
filein_content = loads(fin.read())
for item_mask in filein_content['masklist']:
items.append(ItemMask(item_mask['mask'], (item_mask['charset1'], item_mask['charset2'],item_mask['charset3'],item_mask['charset4'])))
return items
if __name__ == '__main__':
"""
> test.json
{
"masklist": [
{
"mask": "?l?d?d?d?l",
"charset1": "",
"charset2": "",
"charset3": "",
"charset4": ""
},
{
"mask": "?a?a?a?a?a",
"charset1": "",
"charset2": "",
"charset3": "",
"charset4": ""
},
{
"mask": "?a?l?d?a?a",
"charset1": "",
"charset2": "",
"charset3": "",
"charset4": ""
}
]
}
"""
filein = './test.json'
items_mask = file_to_items(filein)
result_incompatibilities = get_incompatibilities_mask_type(items_mask)
print(result_incompatibilities)
# {'?l?d?d?d?l': ['?a?a?a?a?a'], '?a?a?a?a?a': ['?l?d?d?d?l', '?a?l?d?a?a'], '?a?l?d?a?a': ['?a?a?a?a?a']}
Genetic optimizer
solutions = List[]
store_all_solutions(solutions, Items)
remove_incompatibilities(solutions, Incompatibilities)
get_max_valuable_solution(solutions)
sorted_items = sort_ratio_value_weight(Items)
solution = Solution(items=List[], total_value=0, total_weight=0)
for item in sorted_items:
if solution.total_weight + item.weight <= max_weight:
solution.add_item(item)
solution.add_weight(item.weight)
solution.add_value(item.value)
population_size = 100
threshold_max_population = population_size * 3
max_generations = 1000
crossover_probability = 0.9
mutation_probability = 0.25
backpack_capacity = list[Items].length
chromosomal_base = result of the greedy algorithm
avoid_local_max_every = max_generations * 0.05
Population generation
Iterate through generations
- parent fitness computation
- parent selection
- crossover
- child fitness computation
- current best individual selection
- 10% of the new population is generated using the best 10% of the previous population, based on the postulate that if we select only the best individuals, the potential of a population will increase. However this method can increase the probability of reaching a non optimal local maximum.
- The remaining 90% is generated by randomly choosing individuals in the parent population, where the probability of choosing a given individual is proportional to its fitness.
Solver approach
To summarize, generated strategies are quickly created, don't require a technical expertise and they are adapted to time constraints (hashformats, salts). However, they require data on past attacks so they can't be used at first.
Experiments
Generation time
| Worker | Algorithm | Generation time (sec) | Selected attacks | Strategy time (hour) | Max time (hour) |
|---|---|---|---|---|---|
| John | Genetic | 19.095 | 42/46 | 2.848 | 2.85 |
| John | Solver | 0.590 | 40/46 | 2.626 | 2.85 |
| Hashcat-other | Genetic | 45.568 | 110/117 | 1.975 | 2.28 |
| Hashcat-other | Solver | 24.568 | 109/117 | 1.693 | 2.28 |
| Hashcat-mask | Genetic | 13.463 | 24/31 | 0.305 | 0.87 |
| Hashcat-mask | Solver | 0.091 | 24/31 | 0.305 | 0.87 |
Results on a real case

We managed to crack reach the hashes.org "score" in a bit less than 12 hours after uploading the leak to the development box.
From this hashlist, a 5-hour strategy has been generated using the genetic algorithm. The goal is to compare its effectiveness with those of the existing strategies.

| Strategy | Time required | % cracked |
|---|---|---|
| Generated | 4.82h | 87.20 |
| Bruteforce | 6.93h | 08.31 |
| Wordlists | 1.23h | 79.01 |
| Mixed | 5.60h | 48.21 |
Conclusion
- Recon / OSINT / Leaks / Public wordlists / Cracking assets
- Cracking strategy
- Analyze cracked hashes (statistics, common masks, ...) , adapt assets and launch a new strategy
