Quantum readiness: Hash-based signatures
Building robust digital signature algorithms is one of the main challenges in post-quantum cryptography, as classical signatures such as ECDSA and RSA are broken by quantum computers. Thankfully, in the past decades, the academic field has come up with multiple quantum-resistant algorithms which are now being standardized and implemented in modern software. This article highlights XMSS and SPHINCS+, two digital signature algorithms which rely on the well-known robustness of hash functions against quantum computers. However, each one comes with its set of precautions and blind spots, which must be kept in mind when incorporating them in your software.
Looking to improve your skills? Discover our trainings sessions! Learn more.
Why use hash functions in a post-quantum world ?
As explained in our introductory article Quantum readiness: Introduction to Modern Cryptography, hash functions can be modelled as random oracles1 (one can think of a deterministic function which associate each input to a random sample of its output space). In a pre-quantum world where hash queries are performed one at a time, the following properties can be derived for a random oracle $H$ (and thus an ideal hash function) with an output domain size of $2^n$ (n bits):
- given a fixed value $h$, finding a value $x$ such that $H(x) = h$ should take around $2^n$ hash queries. This property is named first preimage resistance
- given a fixed value $x_1$, finding a value $x_2$ such that $H(x_1) = H(x_2)$ should also take around $2^n$ hash queries. This property is named second preimage resistance
- finding arbitrary values $x_1$ and $x_2$ such that $H(x_1) = H(x_2)$ should take around $2^{n/2}$ hash queries (because of the birthday paradox, see the introductory article for more details). This property is named collision resistance
However, in a quantum world in which you can make quantum queries to the hash function and receive quantum results, Grover’s algorithm accelerates these search problems. The new bounds given by this algorithm are as follows:
- breaking preimage and second preimage resistance now take around $\sqrt{2^n} = 2^{n/2}$ quantum hash queries
- collision resistance now takes around $2^{n/3}$ quantum hash queries (see the introductory article and the BHT algorithm2 for more details on this speed-up)
As one can see, while the quantum acceleration is non-negligible, the problem remains a “hard” problem to solve. Using an output domain of 256 bits should still provide you with at least 85 bits of security against a quantum computer.
On a side note, all signature schemes already make use of hash functions. Indeed, to be able to sign arbitrarily long message, it is common for digital signature schemes to sign a hash of the message instead. As such, these signature schemes also rely on the security of hash functions under the hood. Building a signature scheme which only relies on hash function thus removes other potential points of failure in the security model, such as the choice of potentially weak prime numbers or group generators in other schemes.
From a hash function to a signature scheme
In this section, we will build an intuitive idea of how to construct a signature scheme from a hash function. This will be a step-by-step process: first, we will tackle how to sign a single one-bit message, which will enable us to construct a single-use scheme to sign arbitrarily long messages, that we will refine in the following parts. Finally, we will craft a many-times signature scheme based on our single-use algorithm.
Properties for our signature scheme
As a reminder, a digital signature scheme consists in three generic functions3:
- a key generation algorithm, with no defined input, generating a random key pair $(S, P)$, with $P$ being the public part and $S$ the private part
- a signature algorithm, with inputs $m$ (message) and $S$ (private part of the key pair), generating a signature $sig$ for the message $m$ under the key $S$, verifiable with the corresponding $P$
- a signature verification algorithm, with inputs $m$, $sig$ and $P$, outputting a boolean value representing the validity of $sig$ on $m$ with the key $P$
This signature scheme must ensure the following properties in order to be considered secure:
- authentication: it is impossible to forge a signature for a message $m$ under public key $P$ without knowing the private key $S$ associated with $P$
- non-repudiation: given a message $m$ and a valid signature $sig$ under public key $P$, the emitter of $P$ (owner of the associated $S$) cannot deny having emitted a signature for $m$
With that said, feel free to come back to this paragraph at any point to verify that the algorithms discussed later comply with these properties.
Sign one bit, once
Let us consider an easier problem to begin with: how would you sign a single message, made of a single bit ? As a proposition, the following scheme should match the criteria of a digital signature scheme:
- Key pair generation:
- Pick two random bitstrings of arbitrary length $S_0$, $S_1$ (these will form your secret key)
- Compute $P_i = H(S_i)$ for i = {0, 1}. $P_0$, $P_1$ is your public key
- Signature of bit $b$: simply reveal $sig := S_b$
- Signature verification by a third party: check if $H(sig) \stackrel{?}{=} P_b$
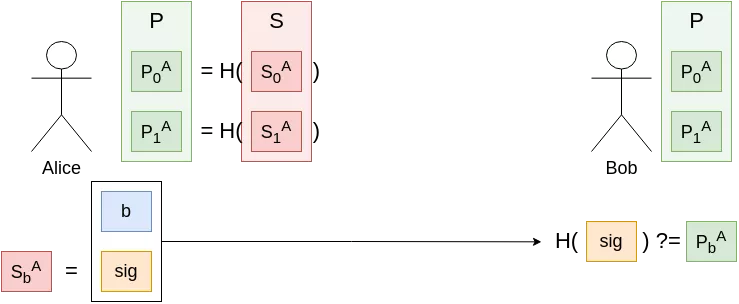
We can check that it is indeed a valid signature scheme; before Alice signed anything, it was impossible for anyone (given the hash function $H$ is first-preimage resistant) to forge a signature in her name, valid under her public key. Even after signing the bit $b$, it is still impossible for an attacker to sign any other message (in this case, the only other possible message is 1-$b$, i.e. 0 if $b$ was 1 or 1 if $b$ was 0).
Why is it called a one time signature scheme ? Let's say Alice uses the same key pair to sign the other possible 1-bit message $b’ = 1-b$, so she reveals $S_b’$. Now she has leaked all of her private key material and our signature scheme is rendered useless.
Sign many bits, once
Lamport Signatures4
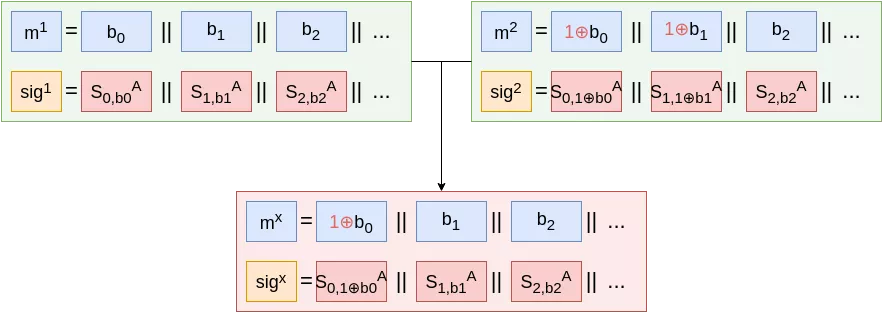
From our one-time one-bit signature scheme, one trivial approach to build a one-time n-bits signature scheme would simply be to generate $n$ key pairs $SuperS := [S_{i,j} := Random() \, | \, i = \{1, …, n\}, j = \{0,1\}]$, $SuperP := [P_{i,j} := H(S_{i,j}) \, | \, i = \{1, …, n\}, j = \{0,1\}]$. Alice could publish $SuperP$, and to sign a message $m := b_1 || b_2 || … || b_n$ she would reveal all the $S_{i,b_i}$ for i = {1, …, n}. As long as each $(S_i, P_i)$ pair (and thus our $(SuperS, SuperP)$ pair) is only used once, this scheme inherits the security properties of our previous one-time one-bit scheme.

Note that here, signing a second message would not necessarily leak Alice’s full secret key. However, assuming at least a two-bits difference between two signed messages $m_1, m_2$, an attacker could forge signatures for messages she did not produce, by picking signatures for each individual bit.
We are still left with an elephant in the room: the keys and signatures sizes are rather large, to say the least. Indeed, let's say Alice wants to sign a 256 bits message, with 85 bits of PQ security, using SHA256 as her base hash function:
- for each bit she wants to sign, she has to store two sufficiently-long bitstrings (around 170 bits each) to ensure the hardness of finding a preimage: $256*2*170$ bits ≈ 87 Kb.
- her public key, consisting of all the hashes (outputs of SHA256 for example) of the secret bitstrings, would be $256*2*256$ bits ≈ 131 Kb. This has to transit over the network.
- a signature would take up half the size of the secret key, so 44Kb, and would transit over the network.
Winternitz One Time Signatures (WOTS)
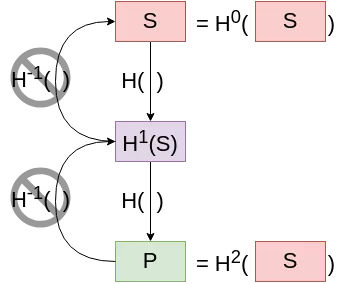
In order to reduce the key and signature sizes, we could improve on our initial primitive (the one-time one-bit signature scheme), at the cost of a small overhead in computation time. Indeed, instead of two secrets, we could try and use only one secret $S$, with our public key $P$ being $P := H^2(S)$. This concept will be referred as a “hash chain” for the rest of this article. Signing the bit $b$ would translate to revealing $sig := H^b(S)$.
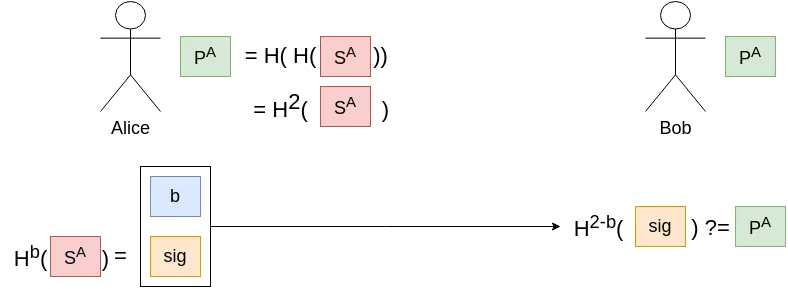
However, with that scheme, even if the secret is used only once, if the signature $sig_0$ of the message 0 is revealed, an adversary could easily compute $sig_1 := H(sig_0)$, effectively advancing the hash chain. We thus need to append a checksum, which would ensure that going forward on a chain in the message section would mean going backwards in a chain in the checksum section. Instead of signing only $b$, we will add $c := 1-b$ and sign $m = b||c$. As our new message is 2-bits long, we will need two keys: one hash chain key-pair for the 1-bit message $b$, and a second one for the 1-bit checksum $c$.
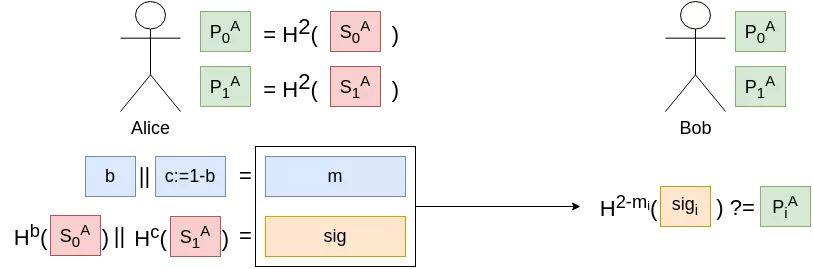
Back with two secret bitstrings and two public hashes to sign a single bit, so we added a few hashes computations and achieved nothing ? Actually no, this new scheme scales nicely in two directions.
Let's say we were to use longer hash chains; instead of signing 1-bit messages (with a chain of length 2 ($=2^1$)), we want to sign $k$-bits message. We keep our secret bitstring $S$, but now the public key $P$ becomes $P := H^{2^k}(S)$, and the checksum formula becomes $c := 2^k - 1 - m$.
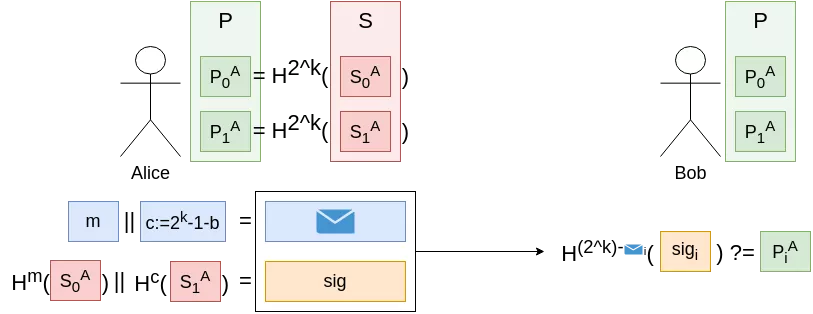
In research papers, you will most often see references to $w = 2^k$ rather than $k$ directly.
Cool, so we can now sign arbitrarily-long messages (by increasing $k$ as much as we need). What is the time complexity ? In order to sign a $k$-bits message, you would need $O(2^k)$ calls to the hash function, and same applies for signature verification. This is really unpractical, so we have to keep $k$ in a reasonable range if we want our scheme to be usable.
Thankfully, the second direction in which our new scheme scales nicely will help us to keep $k$ in a reasonable range. If we were to sign $n$ $k$-bits messages (or rather a message $m$ of length $n*k$ split into $n$ blocks of length $k$, noted $m_1$, … $m_n$) but group their checksum calculations, the checksum formula becomes: $c := \sum_{i = 1}^{n} (2^k - 1 - m_i)$. Advancing in a message block still means going backwards in the checksum (or going backwards in another message block), and this new checksum has a bit-length of $ceil(log_2(n)) + k$ (as the sum of $n$ $k$-bits integers). The total number of blocks to sign in this scheme thus is $n + ceil(\frac{log_2(n)}{k}) + 1$ for a $n*k$ bits message. As an example, here is what signing a 256 bit message (with $n=64, k=4$) would look like:
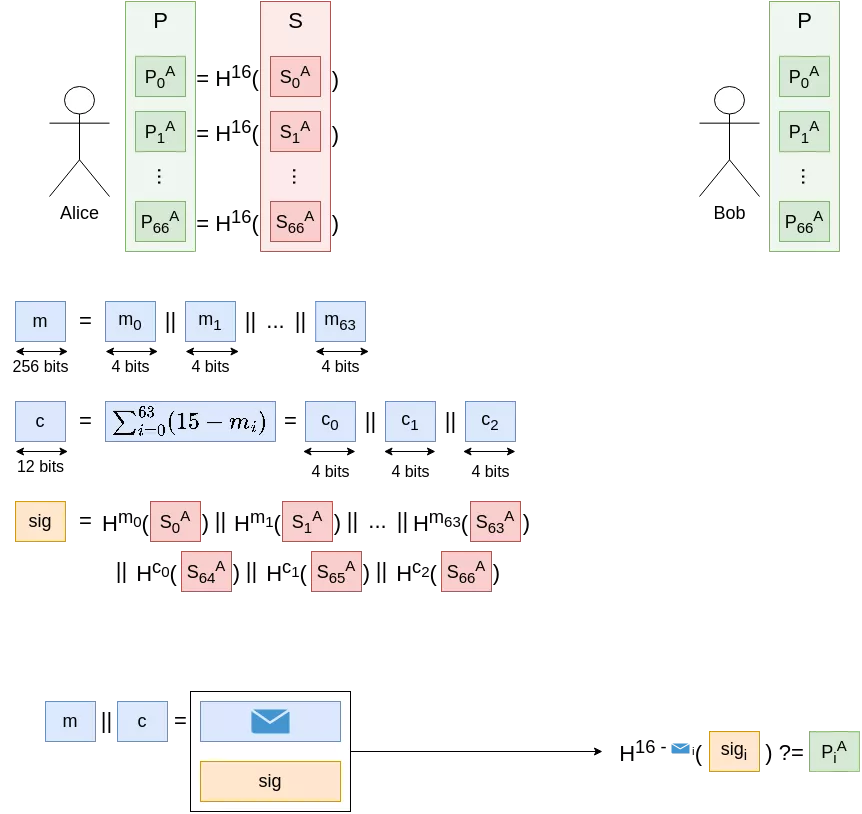
In order to sign a $n*k$-bits message, $O(n*log_2(n)*2^k)$ calls to the hash functions must be performed, which is fine because we can balance growth in $k$ (very expensive) with growth in $n$ (much less expensive). The private and public keys are composed of $n + ceil(\frac{log_2(n)}{k}) + 1$ values, to be able to sign the message and the checksum.
Optimizing secret-key storage
One optimization is left to cover. To generate our WOTS key pair, we need to generate multiple random secret bitstrings ($n + ceil(\frac{log_2(n)}{k}) + 1$, as we saw). But, as a hash function can be considered a random oracle as we have seen in the first article, we can simply generate those secret bitstrings using a hash function in “counter” mode. As such, we would only have to store one secret, and generate all the keys as $S_i = H(secret || i)$.
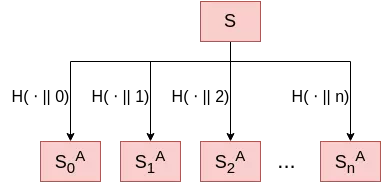
However, such an optimization comes with a risk: all our private keys are now related. If an attacker is able to recover the correct preimage of $S_i$, they can generate all subsequent private keys. To mitigate this issue, a better generation algorithm would use a Key Derivation Function like PBKDF2 in place of the simple keyed hash.
Sign many bits many times - Merkle Signature Scheme
With our fine-tuned one-time signature scheme in hand, it is now time to craft a many-times signature scheme.
While it may seem uncommon to talk about a scheme with security properties only holding for a finite number of signatures under the same keypair, it really is the case with all digital signature schemes5. Indeed, the potential for failure of any digital signature scheme rises over time, due to multiple reasons. For example, after signing a very large number of messages under the same key, the chances of finding a message $m’$ whose hash is colliding with a previously signed message $m$ increases, and hashing the message is the first step of many digital signature schemes. In this case, the non-repudiation property breaks, and the signature scheme is not considered secure anymore. As another example, using ECDSA, related or even reused nonces are more likely to occur over a long period of time (think of the birthday paradox when picking 256-bits nonces at random, risks of collisions arise after less than $2^{128}$ signatures). These also break the security of the scheme.
Here again, one naive approach to this problem would simply be to generate many Winternitz one-time key pairs and send all the public material directly. This is deeply impractical and does not scale nicely towards a larger “many”. Instead, Ralph Merkle came up with an elegant solution to compress this approach: generate a binary tree from all the Winternitz public material by hashing pairs of adjacent nodes, and only publish the root of your tree.
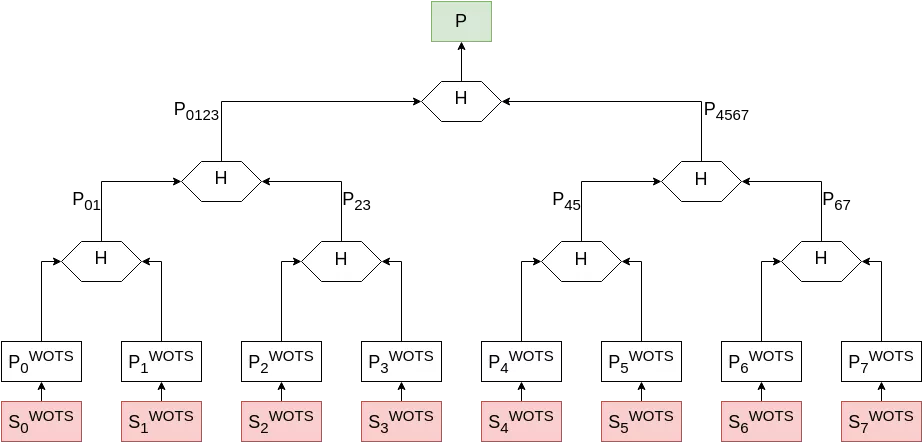
Note that in this schema, the $S_i^{WOTS}$ / $P_i^{WOTS}$ correspond to the large $S$ and $P$ bundles of the previous paragraph on Winternitz signatures. Also, while only 3 tree layers and $2^3$ = 8 key pairs are represented, trees like this can go much higher and larger.
From this model, we can derive our three routines:
- key generation: Alice generates $2^n$ WOTS key pairs. She then constructs the tree structure by repeatedly hashing adjacent public material (as demonstrated above), until only one value remains. The Merkle key pair is $([S_0, S_1, …, S_{2^n}], P)$.
- signature: Alice picks a WOTS secret key which has not been used yet (let's say key 0 for the example), and signs her message using classic WOTS, as seen above. Her Merkle signature will then include the adjacent node public material, along with all the intermediate values needed to re-compute the root of the tree (called the “authentication path”) and the index of the WOTS key pair in the tree (for Bob to know which side to concatenate when checking the authentication path). She then updates her private key, indicating that key 0 has been used and must not be re-used.
- signature verification: Bob computes ${P’_0}^{WOTS}$ from Alice’s message and WOTS signature. He then hashes it along with ${P_1}^{WOTS}$ (included in Alice’s Merkle signature) to recompute $P’_{01}$. Hashing $P’_{01}$ together with $P_{23}$ gives $P’_{0123}$, which can be hashed with $P_{4567}$ to get $P’$. If $P = P’$, the signature is correct.
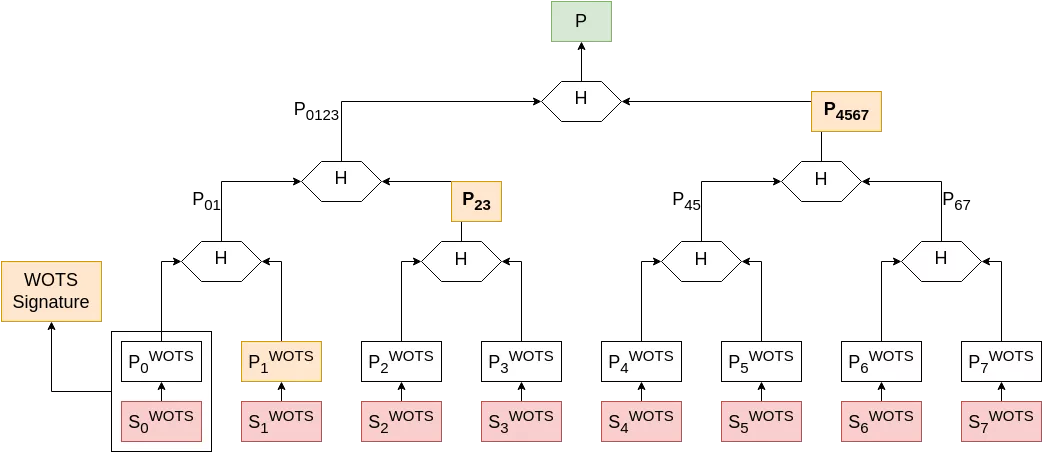
The Merkle private key must keep the information on which WOTS keys have been used, as WOTS is a one-time signature scheme. The simplest way for this is to use the keys sequentially, and store the index of the next unused key. This particularity comes with drawbacks, and will be discussed later on in this article.
With this scheme, the public material can be as small as a single hash value. It turns out that the private part can also be tiny, by reusing the trick detailed in the previous section, Optimizing secret-key storage, to generate all the WOTS key pairs based on a single secret.
However, this scheme comes with a large computational cost to generate each signature. Caching a few upper nodes of the tree could prove valuable, implementation-wise. This can be done without much security considerations as the intermediate nodes are not meant to be secret, and leaking them through a side channel attack or any other way would not break the security of the scheme.
A quick detour: sign many bits a few times (HORS & HORST)
In addition to the constructions presented above, Leonid & Natan Reyzin presented in 2002 a few-times signature scheme6. In such a scheme, even after having signed a single message (and in general after having signed $r$ messages) with a defined key pair, it is still relatively hard to come up with a falsified signature. This is achieved for example with the following construction (named HORS, Hash of a Random Subset):
- First, take two integers $t$ (a power of two) and $k$ (rather small). These are your cipher parameters. HORS proposes $t=2^{10}=1024$ and $k=16$.
- The key pair is composed of $S = (S_0, S_1, … S_{t-1})$ and $P = (f(S_0), f(S_1), …, f(S_{t-1}))$ where each $S_i$ is a random bitstring, and $f$ is a one-way function (a hash function for example)
- To sign a message $m$:
- First, hash $m$ using a hash function $H$ (not necessarily the same as $f$) which has an output size of $k*log_2(t)$ bits. $h = H(m)$
- Split $h$ into $k$ blocks of length $log_2(t)$, and interpret each one as an integer between 0 and $t-1$. $h = h_1 || h_2 || … || h_k$
- Return $sig = (S_{h_1}, S_{h_2}, …, S_{h_k})$
- To verify the signature of $m$ under $P$, simply hash $m$ with $H$ to get $h$ and check if, for all $1 \le i \le k$, $f(sig_i) \stackrel{?}{=} P_{h_i}$.
Indeed, in this case and with the proposed parameters, after signing a single message, falsifying a signature would require an attacker to find a message whose hash is composed only of the same $h_i$ blocks, which is still a hard problem. Let's run the calculations: after signing $n$ messages, at most $k*n$ out of the $t$ secret values have been revealed. Forging a signature then is equivalent to finding a message $m$ whose hash is only composed of these $k*n$ revealed values. Finding such a message at random (in the model of the random oracle) has probability $p_{n,k,t} = (\frac{k*n}{t})^k$ as it can be modelled by $k$ independent Bernoulli trials, one for each block of the hash of $m$, each with success probability $\frac{k*n}{t}$. The number of bits of security can then be calculated as $log_2(\frac{1}{p_{n,k,t}})$. For recommended values of $t$ and $k$, here is how the security decreases with the number of signature published:
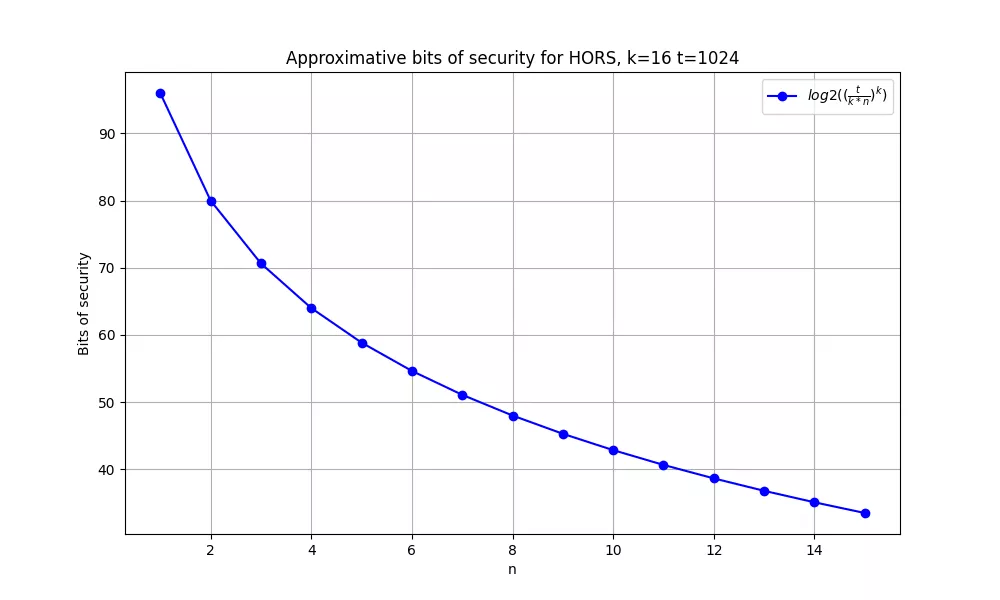
However, this scheme suffers from rather large public keys (composed of $t$ hash values), and a tradeoff can be made by incorporating a binary tree structure into the scheme. Here comes HORST, Hash On a Random Subset with Trees. The $t$ public blocks are hashed two by two (with yet another hash function) in a binary tree, similarly to the Merkle signatures presented above. The public key is therefore reduced to the root of this tree ($O(t)$ decrease in public key size), but the counterpart is that every signature will now need to include the authentication path of each block ($O(k \times log_2(t))$ increase in signature size).
NIST submissions
Now that the building blocks of a hash-based post-quantum digital signature scheme have been presented, it is time to present two schemes part of the NIST standard: XMSS, a stateful algorithm, and SPHINCS+, which can be considered its stateless counterpart. XMSS is recommended by NIST with SP800-2087, and SLH-DSA, a variant of SPHINCS+ has very recently been standardized via the NIST FIPS2058.
XMSS - eXtended Merkle Signature Scheme9 10
XMSS shares a lot with the original Merkle Signature Scheme. In essence, it still relies on multiple one-time signature key pairs, bundled together with a binary tree. However, both the one-time signature scheme and the tree structure slightly differ from the original MSS scheme. These tweaks lead to an improvement on the security of the scheme; rather than needing collision-resistant hash functions like the original MSS, second-preimage resistant hash functions are sufficient for XMSS. The proof of this is detailed in the original W-OTS+ presentation paper.
A more refined OTS - W-OTS+11
W-OTS+ is similar in design to the previously described Winternitz OTS scheme. In order to improve its robustness, the hash chain mechanism is complexified. Instead of using the same hash function to perform every step in the chain, W-OTS+ introduces a unique function for each step. Given a keyed hash function family $f_k$ (a HMAC for example), a key $k$ and a set of “randomization elements” (one random value $r_i$ for each step of the hash chain), the step function at step $i$ takes its input (the output of the step $i-1$, or for $i=0$ the secret bitstring), xors it with the randomization element $r_i$, and hashes the result with the keyed hash function: $c_0 = S, c_i = f_k(c_{i-1} \oplus r_i)$. As the function family $f_k$, the key $k$ and the randomization elements $r$ are all needed in order to walk the hash chain, they need to be known by the verifier and are thus part of the public key ($f_k$ is in fact determined in the W-OTS+ specifications).
Garbled Trees
To more easily represent a W-OTS+ key pair in the main binary tree, the W-OTS+ public key is compressed with a bitmasked binary tree (called an “L-tree” in the literature). In essence, the principle is similar to the randomization elements of W-OTS+; instead of combining nodes by simply concatenating them and hashing them ($n_{i+1,j} = H(n_{i,2j} || n_{i,2j+1})$), random public values $b_{address,side}$ for $side$ in $\{left,right\}$ and $address$ representing the context and index in the tree at which the value $b$ is used, as well as a keyed hash function are added into the mix and the calculation becomes $n_{i+1,j} = H_{k_{address}}(n_{i,2j} \oplus b_{address,left} || n_{i,2j+1} \oplus b_{address,right})$. These values $b$ and $k$ are in fact pseudo-randomly generated from the $address$ and a public seed $SEED$, part of the public key.
While having these values be context-dependant might not seem essential at first, it is in fact critical for the “domain separation” of the hash computation. In short, it prevents an attacker from manipulating and rearranging the nodes of the trees to perform a second-preimage attack, and a lack of it can be rather harmful for the scheme. Please refer to these two excellent articles12 13 for more details on this matter.
Note that, as W-OTS+ keys are made of $n + ceil(\frac{log_2(n)}{k}) + 1$ elements (+ the $r_i$ and $k$) with usual values being $n=64, k=16$ (see the paragraph on the original W-OTS scheme in the previous section for more details), this tree is generally unbalanced. In case a leaf does not have a pair, it is simply copied down to the next layer.
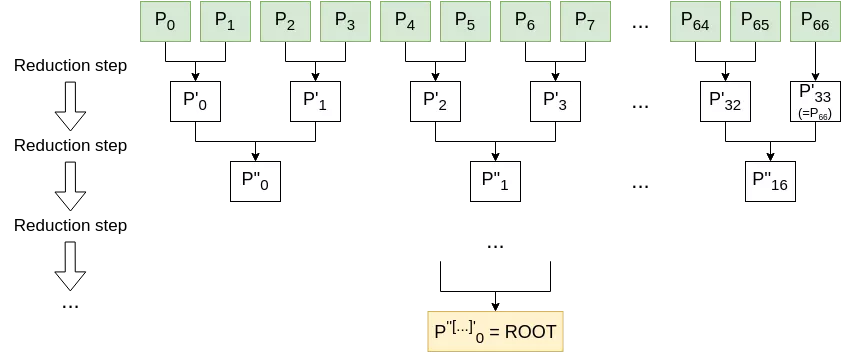
In this schema, each combination step refers to the node combination calculations detailed above. The computed root nodes is then used as the leaf representing this W-OTS+ key in the main tree.
The main tree is also masked using the same pseudo-random node combination procedure. For a visual intuition, you can refer to the schema of the basic Merkle Signature Scheme, simply adapting the node combination algorithm and the leaf nodes.
A stateful private key
While XMSS is great from a theoretical point of view, it comes with a massive implementation challenge. Indeed, as seen earlier with the original Merkle Signature Scheme, the private key must encode the information on the index of the last used OTS key pair. This means that the private key is stateful and has to be updated upon every signature to ensure the security of the scheme. While this poses no issue for a single-threaded, never failing application, this raises many important questions, such as:
- What if the signing application is multithreaded ?
- What if the state is somehow lost or rolls back (for instance due to the restoration of a backup) ?
In all of those cases, the cryptographic scheme is at a high risk of reusing a given W-OTS+ key pair multiple times. This would break the security of the underlying scheme, as an attacker could craft any message having all blocks (both on content and checksum side) after known points in each chain of the reused W-OTS+ key pair. An intuition of such an attack is given with the following diagram:
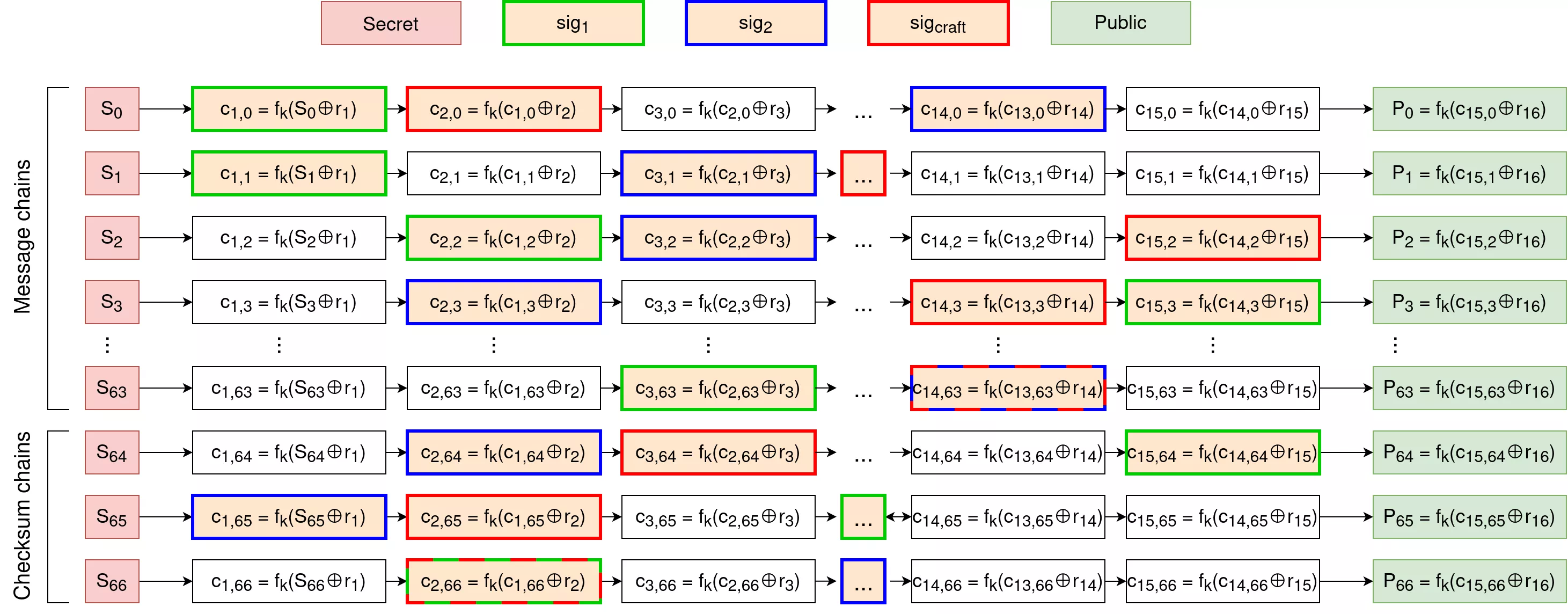
Here, the signature $sig_1$ (in green) of a "small" message reveals early blocks in message chains. However, as we have seen previously with W-OTS, the checksum is here to prevent anyone from crafting a valid signature for a "bigger" message, as this would require knowing earlier blocks in checksum chains. This is where the second signature $sig_2$ (in blue) of a "big" message breaks it all, by revealing early blocks in checksum chains. As such, an attacker can craft the red signature $sig_{craft}$, as they know early blocks both in message chains and in checksum chains.
It is thus vital to ensure that such a reuse cannot occur before deciding to use XMSS. Examples of valid use cases where the private key is sufficiently controlled could be a smart card or a single-threaded IoT device with a proper backup/restore procedure properly maintaining the key state.
SPHINCS+14 15
To eliminate the need for a stateful private key, SPHINCS+ builds on XMSS on two aspects:
- instead of using W-OTS+ as the underlying (one-time) signature scheme, SPHINCS+ uses FORS, a few-times signature scheme which in essence is HORST with a hyper-tree structure (see below);
- instead of a single binary tree like XMSS, SPHINCS+ constructs a hyper-tree made of XMSS trees, with each layer signing the roots of the trees of the next layer. The bottom layer signs the FORS public keys. You can think of this hyper-tree a bit like the web PKI, with a “root CA” (the top XMSS tree) signing the public keys of “intermediate CAs” (the XMSS trees below), which themselves sign other intermediate CAs, which finally sign the end server certificate;
Here is a representation of such a hyper-tree, with only two layers represented:
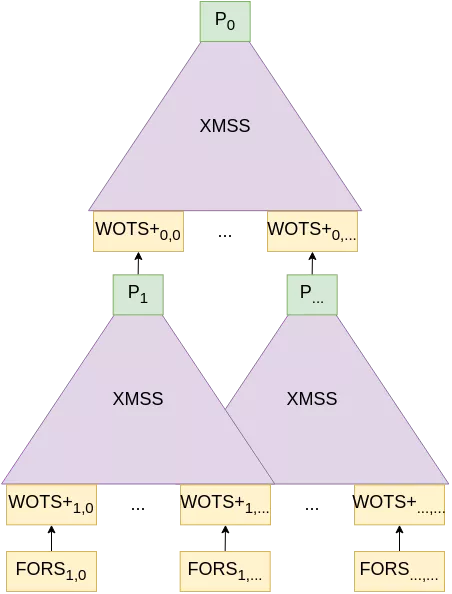
The only thing that needs to be part of the public key is the topmost hash $P_0$ (to further elaborate on our PKI parallel, this would be the root CA certificate), while the private key could consist of a single strong secret, from which everything in this scheme could be derived using the same trick as before (here again, see Optimizing secret-key storage).
The SPHINCS+ signatures include each intermediate XMSS signature along with their authentication path to the next root. Note that these intermediate signatures are constants and could be stored (as the root of a tree only depends on the value of its nodes), but are usually recomputed to ensure the soundness of the signature as well as to reduce the memory footprint of the keys. Because they are constant, the “one-timeness” of the intermediate W-OTS+ keys is not compromised.
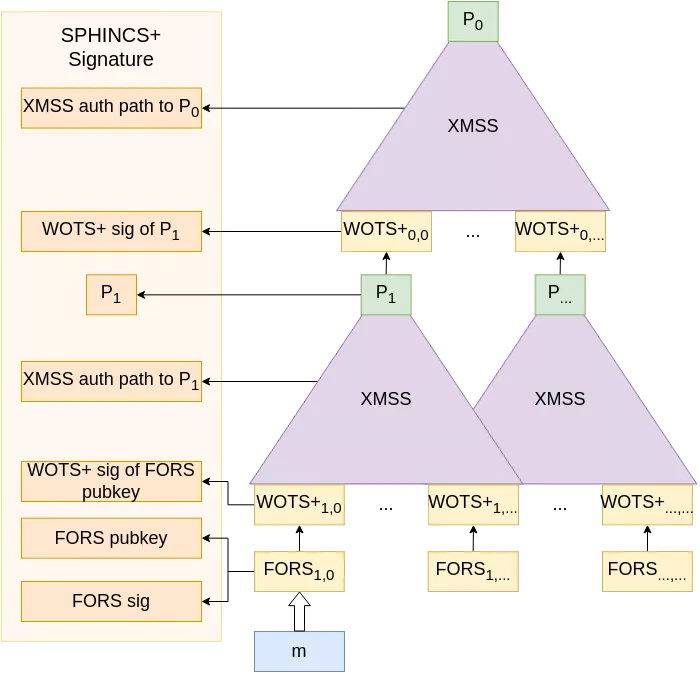
With this new scheme, it is mostly fine to reuse a key pair to sign a different message: indeed, the message signature is performed with a few-times signature scheme. However, using SPHINCS+ to perform a high number of signatures requires a well-balanced picking of all the FORS keys, as the security of each key decreases rather abruptly at each use. To ensure this balanced usage of keys, a pseudo-random function must be used to select the key index upon every SPHINCS+ signature. In practice, a smart PRF choice is the output of a hash function on the message to sign. This has the benefit that signing the same message over and over again does not leak extra key material from other leaves. However, even with the most balanced key usage, the security of SPHINCS+ decreases over time, and it should be kept in mind that the keys must be rotated from time to time. Precise boundaries on that matter can be calculated in the same way we did earlier for HORS(T) (adapting to FORS), adding in the calculations the total number of key pairs, and looking for the number of signatures required to attain too high of a probability for a key to be weakened too much, the exact definitions of those terms being left as exercises to the reader and/or to regulatory agencies.
Fault injections
As presented by Aymeric Genêt, Matthias J. Kannwischer, Hervé Pelletier, and Andrew McLauchlan in 201816, the hyper-tree (sometimes called “multi-tree”) structure of SPHINCS+ is inherently vulnerable to a fault injection attack. As a matter of fact, the intermediate XMSS signatures in the hyper-tree are re-computed every time, based on the public keys of the subtrees below which are supposed to be constants. However, if one were to inject a fault during the computation of a tree root, the following W-OTS+ signature would be performed on a faulty message. Therefore, the attacker would be in possession of two distinct messages along with their signatures with the same W-OTS+ key pair, essentially compromising this key pair as shown earlier. They would then be able to generate a subtree of which they could sign the root with the compromised W-OTS+ key, and craft arbitrary SPHINCS+ signatures from this tree.
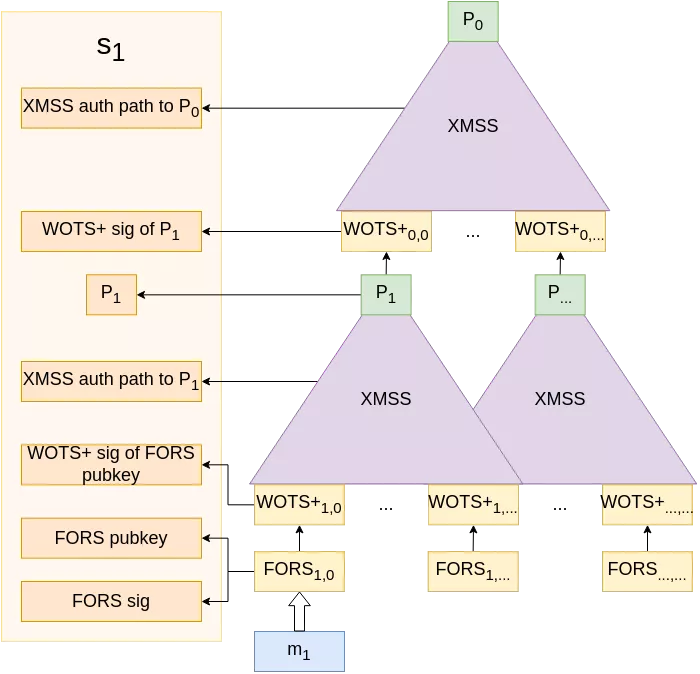
More visually, here is how the attack unfolds. Imagine Alice has access to a target device performing SPHINCS+ signatures on two messages $m_1$ and $m_2$.
|
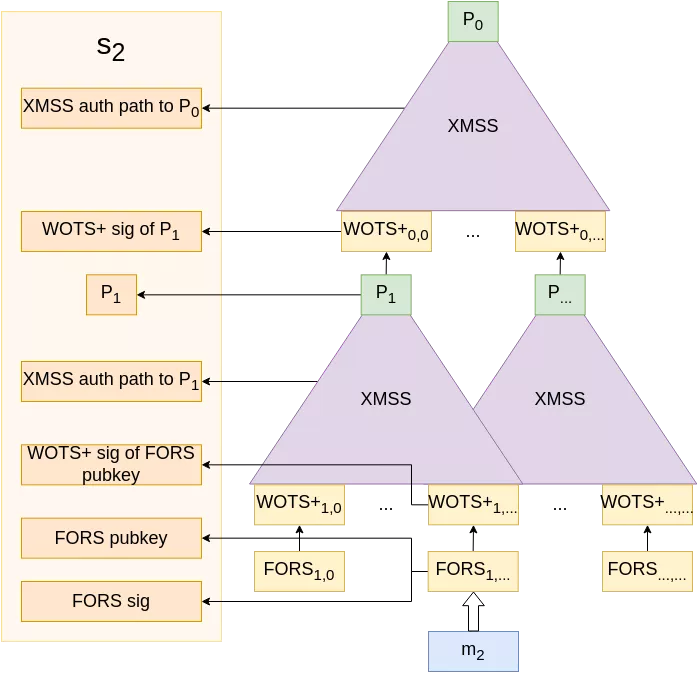
|
Because she wants to impersonate that device, instead of letting the signature of $m_2$ compute normally, she performs a malicious fault injection (via a voltage glitch, an EM pulse, or any other technique) at any time during the calculation of the authentication path to $P_1$, causing it to be miscalculated to a new value $P_1^⚡ \neq P_1$. Now, the same W-OTS+ key that previously signed $P_1$ will sign $P_1^⚡$, and is thus compromised.
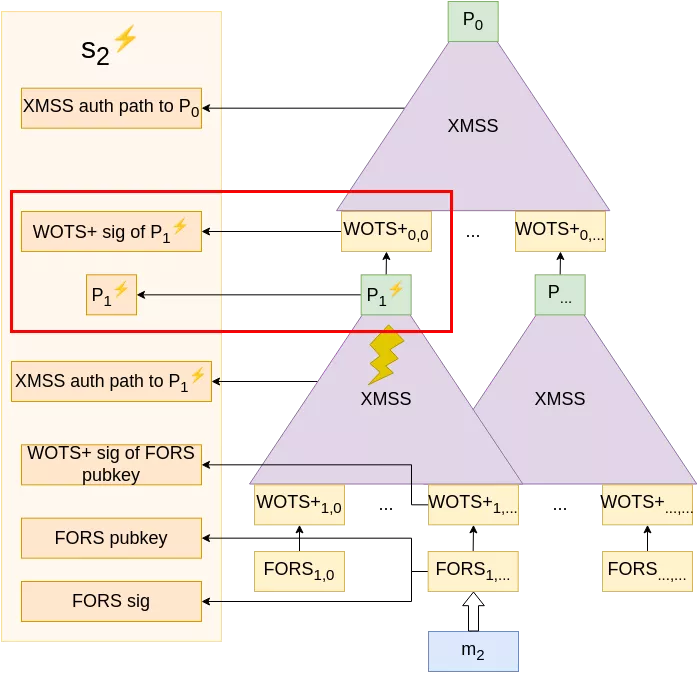
From that point, Alice can re-iterate this operation to further compromise the W-OTS+ key pair (gaining information on "earlier" blocks in each chain as we saw in the paragraph on XMSS), until she has enough information so that she can comfortably generate her own FORS keys, W-OTS+ keys and corresponding XMSS tree with root $P_1^💀$ of which she can craft a signature with the compromised W-OTS+ key pair.
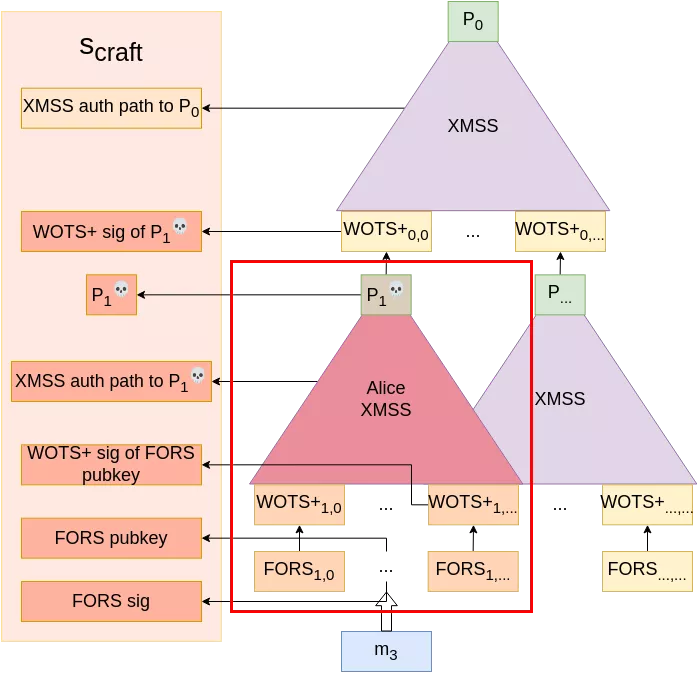
As the topmost XMSS authentication path (to $P_0$) stays the same and every other value can be calculated by Alice, she can successfully craft valid signatures (for messages that map to FORS keys under the compromised subtree) under the device’s public key without knowing its private key. Game over!
In fact, Alice does not even need to try multiple $m_2$ until one falls in the right subtree to conduct the fault injections; if the PRF to select the leaf is the result of a hash function on the input message (as discussed at the end of the SPHINCS+ paragraph), repeatedly querying signatures for $m_1$ and glitching all but one of them would provide 100% success rate.
As such, signature schemes built upon this hyper-tree structure (with intermediate one-time signatures) such as SPHINCS(+) and XMSS^MT (a multi-tree variant of XMSS) should not be used when in fear of hardware attacks. Good thing we still have basic XMSS for these!
- 1. Random Oracle - Wikipedia, https://en.wikipedia.org/wiki/Random_oracle
- 2. BHT Algorithm - Wikipedia, https://en.wikipedia.org/wiki/BHT_algorithm
- 3. Digital Signature - Wikipedia, https://en.wikipedia.org/wiki/Digital_signature
- 4. Lamport Signature - Wikipedia, https://en.wikipedia.org/wiki/Lamport_signature
- 5. NIST Recommendation for Key Management, https://nvlpubs.nist.gov/nistpubs/SpecialPublications/NIST.SP.800-57pt1…
- 6. L. Reyzin, N. Reyzin, Better than BiBa: Short One-time Signatures with Fast Signing and Verifying, https://eprint.iacr.org/2002/014.pdf
- 7. SP 800-208 - https://csrc.nist.gov/pubs/sp/800/208/final
- 8. FIPS 205 - https://csrc.nist.gov/pubs/fips/205/final
- 9. RFC 8391 - XMSS: eXtended Merkle Signature Scheme, https://datatracker.ietf.org/doc/html/rfc8391
- 10. J. Buchmann, E. Dahmen, A. Hülsing, XMSS – A Practical Forward Secure Signature Scheme based on Minimal Security Assumptions, https://eprint.iacr.org/2011/484.pdf
- 11. A. Hülsing, W-OTS+ – Shorter Signatures for Hash-Based Signature Schemes, https://eprint.iacr.org/2017/965.pdf
- 12. P. Junod, Hashing Apples, Bananas and Cherries, https://crypto.junod.info/posts/recursive-hash/
- 13. er4hn, Second Preimage Attack against Merkle Trees, https://er4hn.info/blog/2022.10.08-second_preimage_on_merkle_tree/
- 14. SPHINCS+ Specifications v3.1, https://sphincs.org/data/sphincs+-r3.1-specification.pdf
- 15. SPHINCS+ initial presentation slides, https://csrc.nist.gov/CSRC/media/Presentations/SPHINCS/images-media/SPH…
- 16. A. Genêt, M. J. Kannwischer, H. Pelletier, A. McLauchlan, Practical Fault Injection Attacks on SPHINCS, https://kannwischer.eu/papers/2018_hbs_fa_20181015.pdf
