Quantum readiness: Hybridizing key exchanges
Following our previous article on signatures hybridization, this article covers the basics of hybridizing your key exchanges to ensure maximal security of your data.
Looking to improve your skills? Discover our trainings sessions! Learn more.
More urgently than digital signature schemes, the way we exchange shared secrets on the internet needs to transition to the post-quantum era. Because of a relatively insufficient hindsight regarding new “post-quantum” key exchange schemes, most institutions incentivize the use of hybrid schemes, combining the robustness of renowned classical schemes with the post-quantum protection offered by newer schemes. This blogpost details the state of the main concepts of hybrid key exchanges.
Quick recap: definitions
Key Encapsulation Mechanisms
Calling something a Key Encapsulation Mechanism (KEM) is just a fancy way of referring to a generic solution to a problem you already know : how can Alice and Bob share a secret through a public channel? In classical cryptography, this problem is solved with a Diffie-Hellman key exchange: Alice and Bob publish their respective public keys, and mix their private key with each other’s public key to land on the same secret value, which only they can know. In post-quantum cryptography, various techniques exist to establish this shared secret, some of which have been discussed in a previous article about lattice-based schemes1.
A Key Encapsulation Mechanism is defined by three routines:
KeyGen(), responsible for generating a key pair consisting of a private part and a public part.Encaps(Kpub), responsible for generating a secret value and a “capsule”, which is a blob that can be transformed back into the secret value only by the possessor of the associated private keyDecaps(Kpriv, caps), used to recover the secret value from the capsule, by using the corresponding private key
As an example, a classic Diffie-Hellman (DH) key exchange can be viewed as a KEM, by defining the three routines as follows:
DH public parameters: a generator g
KeyGen(): Pick a random integers. ReturnK_priv = sandK_pub = g ** sEncaps(K_pub): Encaps can be seen as an Ephemeral Diffie-Hellman key exchange. Start by picking a random integerx, then compute the associated public key which will act as your capsulecaps = g ** x, and the shared secretsecret = K_pub ** xDecaps(caps, K_priv): Decaps simply computes the key exchange between the ephemeral public key and our own private key.secret = caps ** K_priv
Hybridization
Hybridization is the practice of combining both post-quantum and classical schemes to obtain a new, more resilient scheme against both classical and quantum attacks. For more details, a more complete definition has already been covered in our previous blogpost about hybridizing signatures. We encourage you to read it, if you haven’t done so already2
Combining KEMs
KEM combiners were studied in depth by F. Giacon, F. Heuer and B. Poettering in a 2018 research paper3. In this paper, they introduce a general construction for combiners, where all the key exchanges are performed in parallel. The actual combination work is performed at the end, as a function W of all shared secrets, capsules and public keys, which outputs the combined shared secret.

In the following parts, we study such functions and provide hindsights into why they may or may not be pertinent choices.
Concatenating the shared secrets
A first approach one might take when it comes to combining many secrets into one is simply to concatenate them all.
- CombiKEM.KeyGen():
S_X, P_X <= KEM_X.KeyGen()
S_Y, P_Y <= KEM_Y.KeyGen()
S <= S_X, S_Y
P <= P_X, P_Y
return S, P
- CombiKEM.Encaps(P):
P_X, P_Y <= Split(P)
ss_X, caps_X <= KEM_X.Encaps(P_X)
ss_Y, caps_Y <= KEM_Y.Encaps(P_Y)
ss <= ss_X || ss_Y <--- W
caps <= caps_X, caps_Y
return ss, caps
- CombiKEM.Decaps(caps, S):
caps_X, caps_Y <= Split(caps)
S_X, S_Y <= S
ss_X <= KEM_X.Decaps(caps_X, S_X)
ss_Y <= KEM_Y.Decaps(caps_Y, S_Y)
ss <= ss_X || ss_Y <--- W
return ss
However, there are a few reasons why this might not be the best thing to do:
- the length of the final shared secret varies with the number of combined KEMs and their output sizes
- if one of the KEMs was to be broken, the final shared secret would be partially known to an attacker. As such, it would not entirely be “secret” anymore
Ideally, breaking all but one KEMs in our combiner should not give sufficient information to guess parts of the final shared secret. Intuitively, we want our KEM to diffuse the entropy that each KEM brings to all the bits of the final shared secret.
Concatenating the shared secrets, then hashing
With the previous lessons about entropy diffusion learned, one can think of the following combiner as a next iteration:
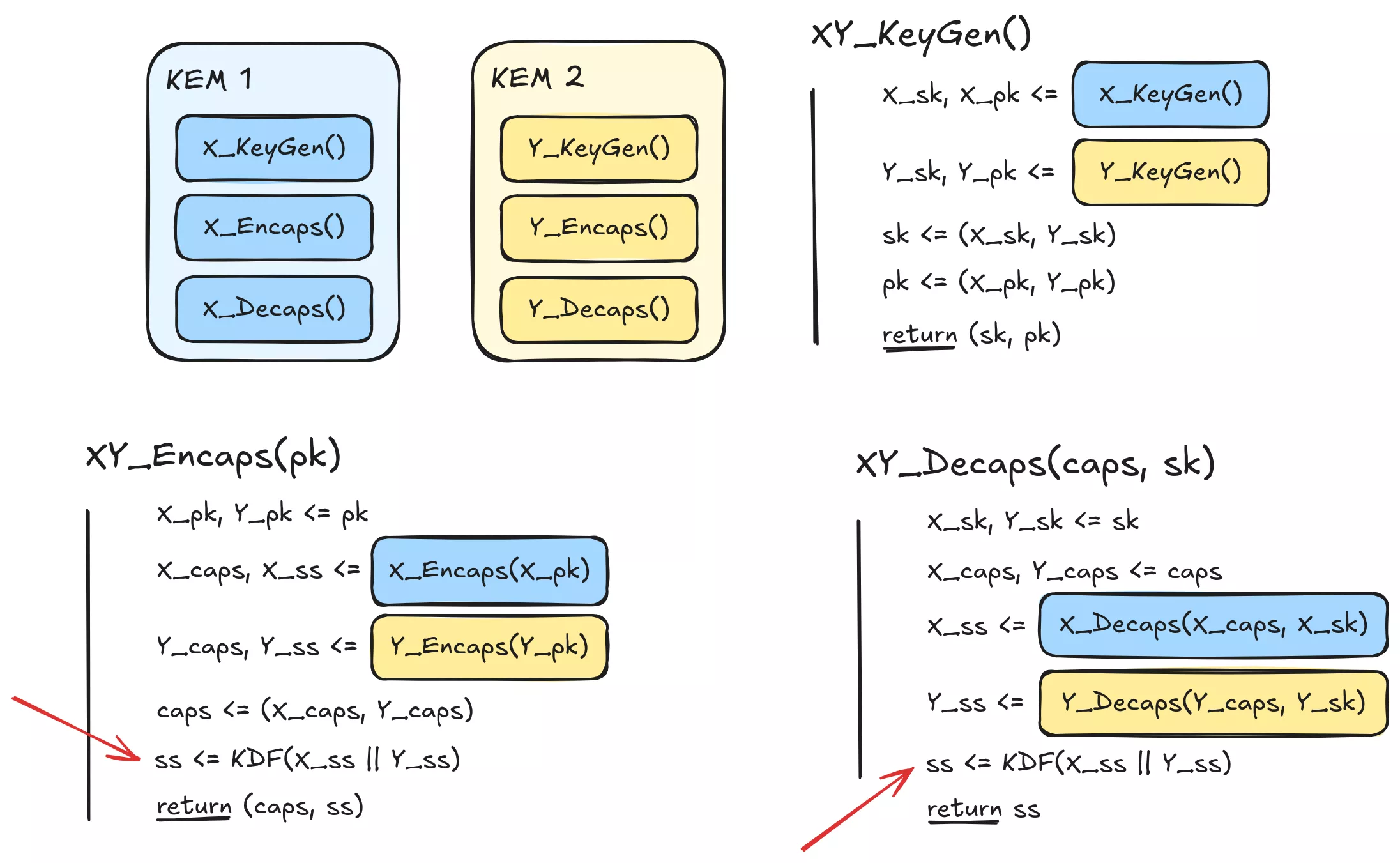
This combiner concatenates and then performs a key derivation operation (for example with a hash function) on the shared secrets of the component KEMs together to form the final shared secret. This ensures that every output bit is dependant on every input bit, in terms of entropy. However, in a world where our ideal combiner must be “at least as good” as each ingredient KEM, this is still insufficient.
To further prove this point, let us examine the notion of “session key indistinguishability” (discussed in two IACR papers3 4). It describes the ability for an adversary to distinguish a shared secret from a random blob, given the corresponding capsule.
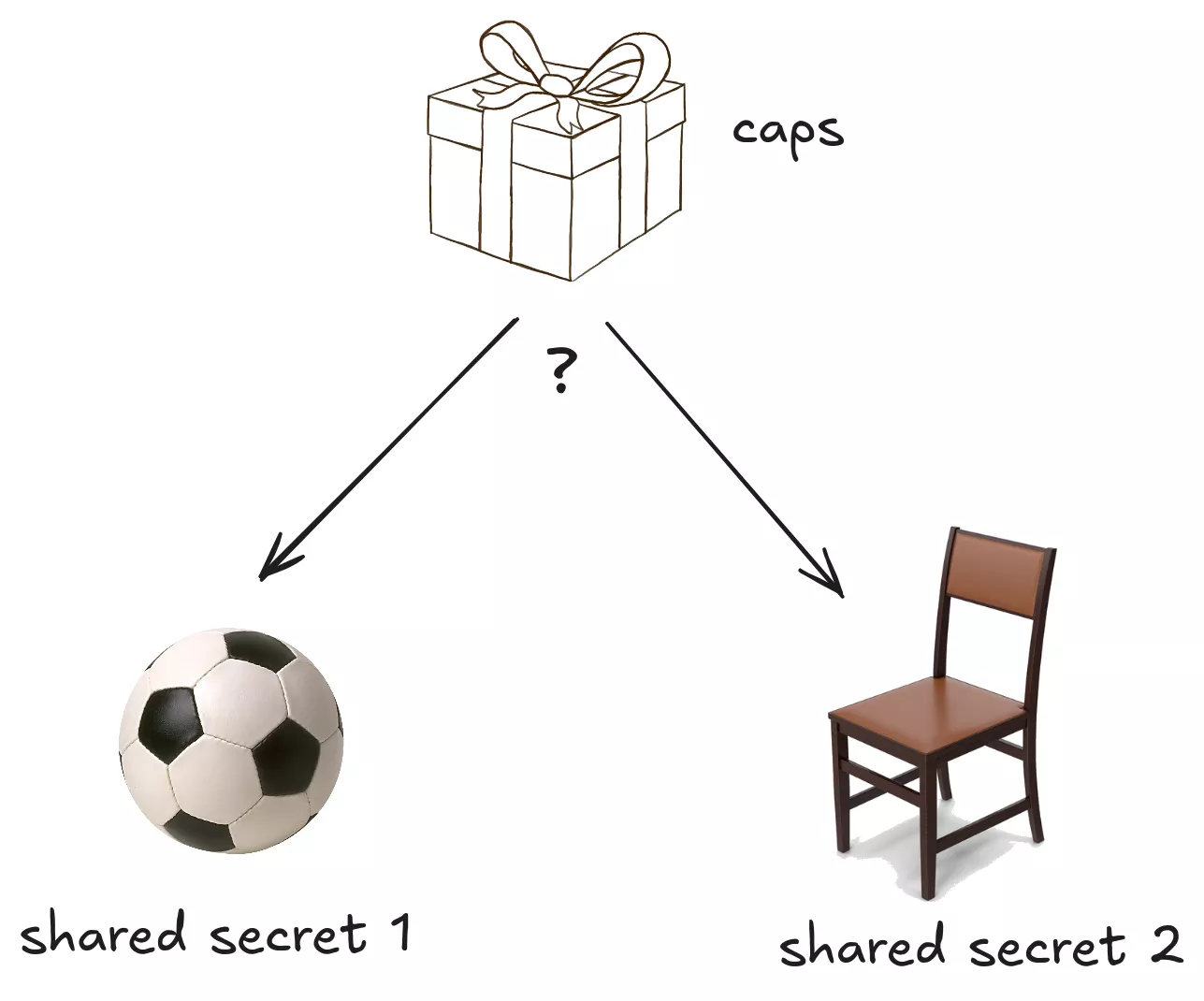
Session key indistinguishability can be thought of as guessing “what is in the box?”, given two possible answers.
We will cover two levels of session key indistinguishability here:
- Indistinguishability against Chosen Plaintext Attack (IND-CPA): The challenger provides a public key, a capsule, its associated shared secret and a random blob. The adversary has access to an Encaps oracle which they may call as many times as they want, with any public key of their choice. At one point, the adversary must decide which one of the provided blobs is the shared secret wrapped by the provided capsule.
- Indistinguishability against Chosen Ciphertext Attack (IND-CCA): The challenger still provides a public key, a capsule, its associated shared secret and a random blob. The adversary now has access to an Encaps(P) and a Decaps(caps) oracle (decapsulation being performed with the same key as the challenge) which they may call as many times as they want, on any input except the provided capsule. At one point, the adversary must decide which one of the provided blobs is the shared secret wrapped by the provided capsule.
To follow our “what’s in the box?” metaphor, you can think of IND-CPA as having access to a gift wrapping machine, allowing you to wrap as many objects as you want before taking your guess about what’s in the original box. IND-CCA gives you access to a wrapping and an unwrapping machine, to which you can ask anything but to unwrap the original box.
A KEM’s security can be qualified with regards to these security properties, and we would like our combiner to be rated to the same session key indistinguishability level as the best ingredient KEM.
Sadly, the concatenate-then-hash combiner does not meet our expectations in the general case. Indeed, let’s consider two KEMs, KEM_X and KEM_Y. Let’s further say KEM_X is IND-CCA secure, but KEM_Y is broken in such a way that it is possible to find capsule/shared secret collisions for a fixed (but secret) private key k, i.e. for a certain caps, find caps′ ≠ caps such that Decaps(caps,k) = = Decaps(caps′,k). We note that KEM_Y is not IND-CCA secure; given a challenge (caps,sA,sB), an adversary can generate a capsule caps′ that collides with caps and then query the decapsulation oracle with Decaps(caps′). The adversary can then win the game using the shared secret returned by the oracle.
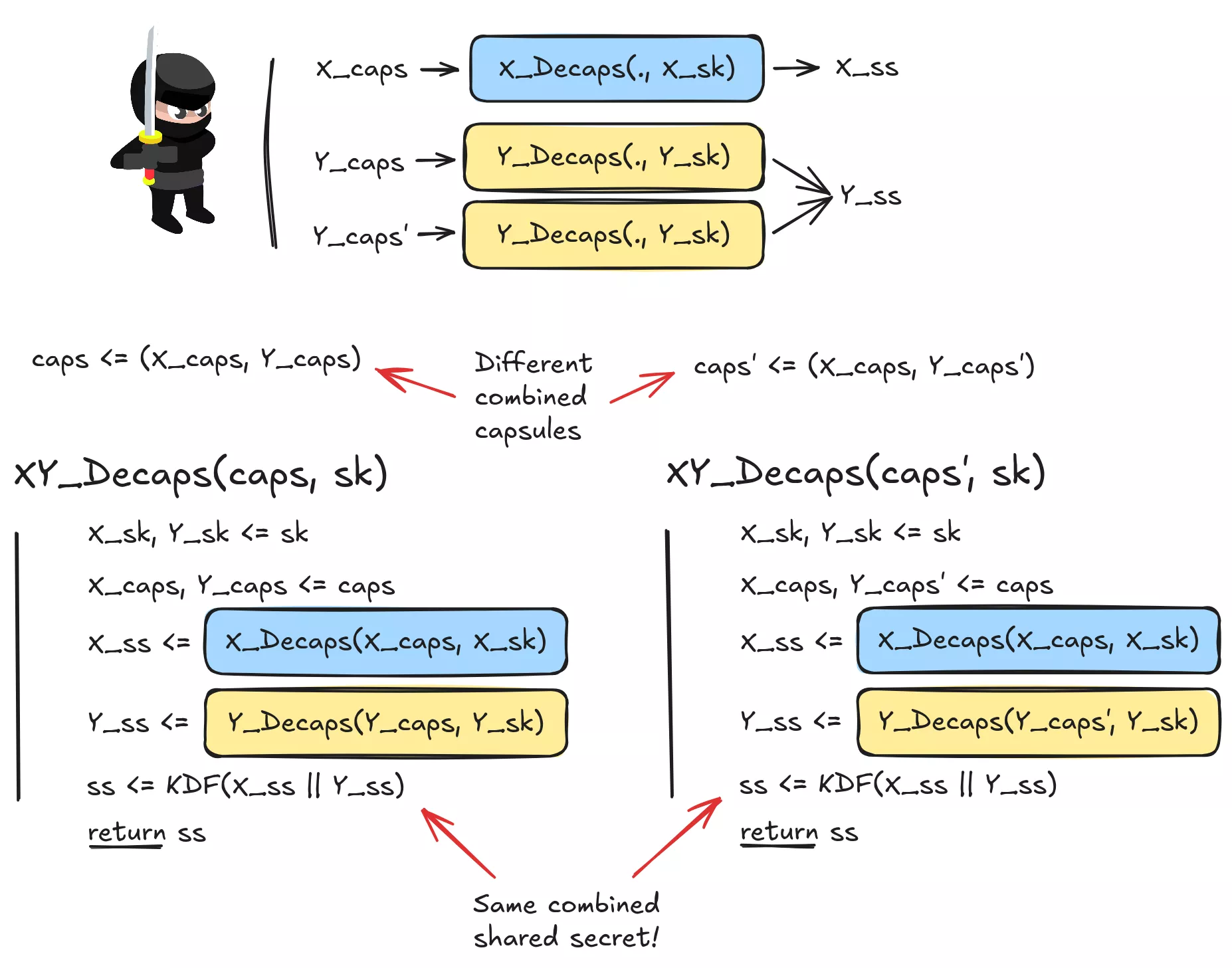
Indeed, when provided with a challenge (caps,sA,sB) (where caps is composed of X_caps from KEM_X and Y_caps from KEM_Y), the adversary is able to craft Y_caps′ ≠ Y_caps which decapsulate with KEM_Y to the same shared secret. Thus, the adversary has two different capsules caps = X_caps, Y_caps and caps′ = X_caps, Y_caps′ which decapsulate with our combined KEM to the same shared secret. With the same argument as for KEM_Y not being IND-CCA, the composite KEM is not IND-CCA while KEM_X is IND-CCA.
Note that a KEM with collisions like KEM_Y in the previous demonstration can be instantiated with a Diffie-Hellman key exchange, given poor parameter choices:
# === DH params
p=1277723 # p = 2*q + 1, with q=638861 also prime
g=3 # order(g) = q
# === KeyGen()
# Alice privkey
a = 130376
# Alice pubkey
A = pow(g, a, p)
# === Encaps(A)
# Bob ephemeral private key
b = 644734
# Bob ephemeral public key
B = pow(g, b, p)
# Shared secret and capsule
ss, caps = pow(A, b, p), B
# === Decaps(caps, a)
assert pow(caps, a, p) == ss
# === Collision !
# Other capsule, colliding (using the fact that `a` is even)
v = 1277722 # order(v) = 2
caps_coll = (caps*v) % p
assert caps != caps_coll and pow(caps_coll, a, p) == ss
As you can see, for a given capsule and a poorly chosen private key, a colliding capsule can be found instantly in this scheme.
Nonetheless, according to M. Barbosa et al. 5, a “concatenate then hash” combination is secure if you can prove the ciphertext second pre-image resistance of the component KEMs. This property was clearly not respected in our example, as KEM_Y was specifically crafted to provide collisions, hence the IND-CCA breakdown of the resulting KEM.
Concatenating shared secrets and capsules and then hashing
For the general case, M. Campagna & A. Petcher’s paper from 20204 proposes to include the capsules and public keys of each KEM to the mix. This addition allows defending against the attack presented in the previous paragraph, as the final shared secrets of the colliding capsules will now differ. However, capsules and keys are much bigger for post-quantum algorithms than they are for classical ones. As such, this construction comes with a non-negligible overhead, in the form of a larger input to the key derivation function call.
To avoid this performance drawback, the IETF’s Composite ML-KEM draft6 proposes a different method. By proving that ML-KEM has ciphertext second pre-image resistance, they can safely omit the large ML-KEM capsule and public key from the KDF input. This approach maintains the required IND-CCA security without the performance penalty.
KemCombiner<KDF>(mlkemSS, tradSS, tradCT, tradPK, Domain) -> ss
[...]
if KDF is "SHA3-256":
ss = SHA3-256(mlkemSS || tradSS || tradCT || tradPK || Domain)
else if KDF is "HMAC-{Hash}":
ss = HMAC-{Hash}(key={0}, text=mlkemSS || tradSS || tradCT || tradPK || Domain)
ss = truncate(ss, 256)
return ss
Combiner function used in IETF’s Composite ML-KEM. Domain is a constant used to indicate which specific pair of algorithms has been combined
Lessons learned
Hybridizing key exchanges offers a prudent path forward, blending the time-tested security of classical algorithms with the future-proofing of post-quantum schemes. However, this article demonstrates that the method used to combine these schemes is as critical as the schemes themselves. We have seen that a simple concatenation of shared secrets is insufficient, and even a more intuitive “concatenate-then-hash” approach can introduce subtle vulnerabilities.
To build a truly resilient hybrid KEM, there are two main paths:
- A general-purpose construction, incorporating not just the shared secrets but also the capsules and public keys from each KEM into the final key derivation function. This is the safer path, but may come at a significant performance cost due to the large size of post-quantum artefacts.
- A more optimized approach, such as the one taken by the IETF for Composite ML-KEM, relies on proving stronger security properties of the component KEMs, such as ciphertext second pre-image resistance. This allows for a more streamlined combination that omits the bulky post-quantum capsules and keys from the hash, achieving high performance without sacrificing security.
In conclusion, designing secure hybrid mechanisms is a nuanced task, be it for signatures or for key exchanges. Developers should rely on standardized and rigorously analysed constructions, like the ones proposed by the IETF, rather than inventing custom solutions relying on intuition alone. These standards provide a trusted blueprint for achieving both high security and practical performance, ensuring that our encrypted communications remain confidential against all adversaries, present and future.
- 1. https://www.synacktiv.com/en/publications/quantum-readiness-lattice-bas…
- 2. https://synacktiv.com/en/publications/quantum-readiness-hybridizing-sig…
- 3. a. b. https://eprint.iacr.org/2018/024.pdf
- 4. a. b. https://eprint.iacr.org/2020/1364.pdf
- 5. https://eprint.iacr.org/2024/039
- 6. https://datatracker.ietf.org/doc/draft-ietf-lamps-pq-composite-kem/
