Quantum readiness: Hybridizing signatures

Cryptographic hybridization is the strategy of choice for a secure transition to the post-quantum era. By combining the proven robustness of current algorithms with the resistance of new standards to the quantum threat, it guarantees optimum protection. However, this dual assurance comes at a cost: a more complex implementation and a non-negligible impact on performance. This article explores the technical considerations and best practices for implementing robust hybrid signatures.

Quick recaps

Signature scheme

While you may be familiar with the concept of digital signatures, a reminder never hurts. A signature algorithm is a cryptographic mechanism used to verify the authenticity, integrity, and non-repudiation of data. It uses asymmetric cryptography, involving a key pair: a private key for signing and a public key for verification. It consists of three routines:

• KeyGen(), in charge of generating a key, made of a private part and a public part.
• Sign(Kpriv, m), taking a private key and a message, and generating a signature for said message.
• Verify(Kpub, m, sig), taking a public key, a message and a signature and checking if the signature corresponds to said message and key.

A digital signature scheme is said to be “secure” when it is computationally hard for an attacker to forge signatures without knowing the associated private key. Various adversary models exist to challenge this assumption1, such as the Existential Unforgeability against Chosen Message Attack (EUF-CMA), in which an adversary has access to an oracle capable of signing arbitrary messages, and needs to produce a signature for a new message which was not previously signed by the oracle. A scheme is thus considered secure with regard to EUF-CMA if no such adversary exist.

Combination and hybridization

In cryptography, a combiner is an algorithm that merges multiple algorithms of the same kind (signature / key exchange) into one, hoping to benefit from all the security properties of individual algorithms. A signature combiner thus takes a number of signature algorithms in input, and generates a new signature scheme, wrapping all the input signature algorithms and being at least as strong as each of them individually, or so we hope.

Hybridization is a special case of combination, where the user combines classical algorithms with post-quantum ones. The primary goal is to create a single, more resilient cryptographic scheme that is secure against both classical and quantum computers. It is required by many institutions such as the ANSSI in France, because of the relative uncertainty about the security of the post-quantum schemes which have been less field-tested and studied.

In fact, this principle of precaution already proved useful and efficient in the past. Indeed, in 2019, a Cloudflare experiment about the post-quantum transition2 assessed the feasibility of using post-quantum key exchange mechanisms in the TLS protocol. They relied on two post-quantum algorithms, SIKE and NTRU-HRSS, which were both hybridized with classical X25519. Later, in 2022, W. Castryk and T. Decru discovered a classical attack on SIKE3 which totally ruined the security properties of this scheme. Had Cloudflare not hybridized this algorithm with a robust classical one, the SIKE key exchanges performed during this 2019 experiment would be trivially broken today by an attacker in a man-in-the-middle position having recorded the TLS communications at that time.

The main advantage of such a generic algorithmic construction is its crypto-agility, meaning that it enables seamless swapping of cryptographic primitives. This helps to mitigate the single point of failure that could be a cryptographic primitive used alone.

As the field of post-quantum cryptography currently prioritizes key establishment and digital signatures, our focus will remain on these two domains. This article delves into the topic of hybrid signatures, while the next in this series will be dedicated to Key Encapsulation Mechanisms (KEMs).

While combiners can theoretically be constructed to assemble n algorithms, we will only cover the (most common) case, where n = 2. Specifically, we will focus on the hybrid model that combines a single classical algorithm with a single post-quantum one.

Combining signature algorithms

Before we start digging into real-world signature combiners, ask yourself a question: how would you combine two digital signature algorithms such that the combination is at least as secure (in terms of unforgeability) as the strongest one ?

The Concat combiner

To the previous question, your intuition might have been: “Let’s just sign the message with both algorithms, send both signatures and verify them all”. And you would be right! Such a scheme is indeed at least as secure as each one taken individually.

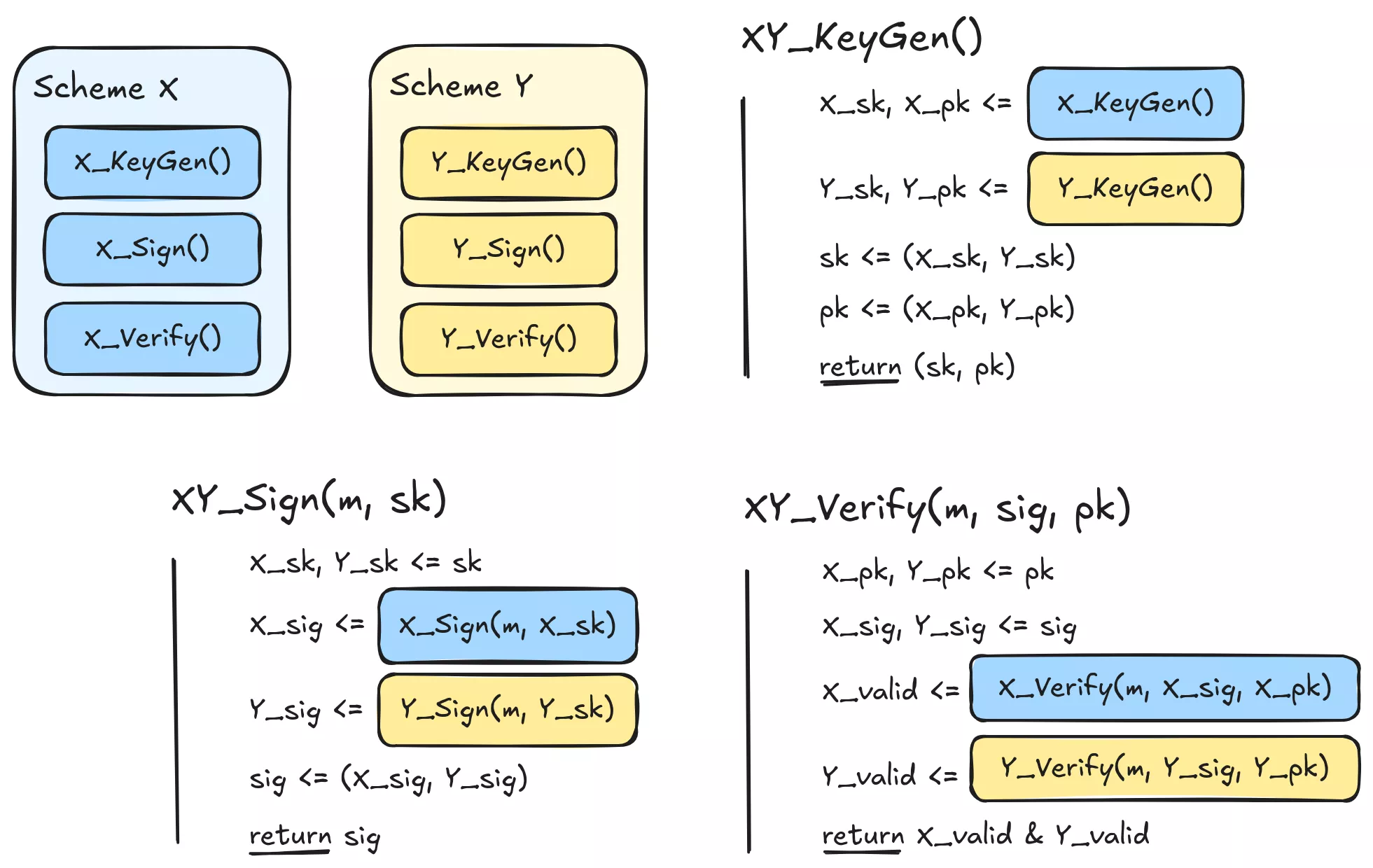
Let’s say Alice sends a signed message to Bob with this combined scheme, made of algorithms X and Y, where at least one of them (let’s say X) is EUF-CMA. In order to forge a signature for a message m in this combined scheme, an attacker would need to forge a signature for m with algorithm X and a signature with algorithm Y. However, as X is EUF-CMA, this task would be unfeasible for the attacker. As such, this signature combiner is also secure with regard to EUF-CMA. More generally, breaking a security property of this combiner requires breaking it for all the underlying algorithms, granting the “at least as secure as each component” property.

As a side note, it is interesting to note that this combiner is the only generic construction recommended by ANSSI for signature combination in their Real-World PQC 2023 slides4.

On separability

Although the previous scheme is interesting in a full-hybrid context, a malicious actor could extract a single signature (be it the one with X or with Y) and use this signature by itself without any evidence that it was initially part of a hybrid signature, thus deviating from Alice’s original hybrid intent. This could happen if the verifier also accepts signatures with only X or Y using parts of the hybrid key, for compatibility reasons for example. This property is called “separability”, and is discussed in great details in a 2023 paper by N. Bindel and B. Hale5.

The researchers highlight two levels of non-separability: first is weak non-separability, where signatures are still performed independently from one another, and the “evidences of hybridization” are implemented at the protocol level. Examples of such evidences could be:

• Using the IETF’s Composite Signatures draft6, which is roughly equivalent to using the Concat combiner to sign "HYBRIDSIG"||m
• Using a dedicated key, specifically published for hybrid signatures (with a specific Key Usage attribute in the certificate for instance)

A stronger level of non-separability (called strong non-separability) is also presented. This time, the artefacts are implemented at the algorithm level. An example of strongly non-separable scheme, adapted from the paper for simplicity reasons and combining a Fiat-Shamir-based scheme (such as the post-quantum scheme ML-DSA) with RSA is as follows:

Here, the RSA signature is not directly related to the message and is meaningless by itself, and the Fiat-Shamir signature is incomplete without the RSA data. This scheme is thus strongly non-separable, as it is impossible to verify a component signature without involving the other algorithm. Moreover, it still remains “at least as strong” as the individual signature algorithms (but the proof is left as an exercise :D). For more details on schemes like this one, please refer to the original paper.

Apart from stopping an attacker from isolating a sub-signature, strong non-separability may also save you from implementation mistakes like the following:

import threading

def verify_X(key, message, signature):
    global valid
    isXValid = True # do stuff to verify signature with X
    valid &= isXValid

def verify_Y(key, message, signature):
    global valid
    isYValid = True # do stuff to verify signature with Y
    valid &= isYValid

key = "aaa"
message = "bbb"
signature = "ccc"

# Global "valid" variable
valid = True

thread_x = threading.Thread(target=verify_X, args=(key, message, signature))
thread_y = threading.Thread(target=verify_Y, args=(key, message, signature))

# Start verification threads
thread_x.start()
thread_y.start()
# Wait for both threads to return
thread_x.join()
thread_y.join()

print(f"Hybrid signature validity is: {valid}")

This code may look fine on the surface (except for a potential race condition which is not relevant here), parallelizing the signature verification for better performances:

$ python3 hybrid_parallel.py 
Hybrid signature validity is: True

However, imagine that for some reason, verify_Y was to raise an exception:

def verify_Y(key, message, signature):
    global valid
    raise Exception() # crash during Y verification
    isYValid = False
    valid &= isYValid

The code would now show the following behaviour:

$ python3 hybrid_parallel.py 
Exception in thread Thread-2 (verify_Y):
Traceback (most recent call last):
  File "/usr/lib/python3.11/threading.py", line 1038, in _bootstrap_inner
    self.run()
  File "/usr/lib/python3.11/threading.py", line 975, in run
    self._target(*self._args, **self._kwargs)
  File "/tmp/hybrid_parallel.py", line 10, in verify_Y
    raise Exception()
Exception
Hybrid signature validity is: True

In this case, while an exception is thrown in the Y thread, it is not fatal to the program and the signature is computed as valid. This could not possibly occur with a strongly non-separable hybrid scheme, where the signatures are mathematically inter-dependent.

However, strong non-separability comes with a crypto-agility challenge. The level of entanglement of the two algorithms involved means that the Sign / Verify routines cannot be treated as black boxes running in parallel anymore, and the necessary tweaks to make a combination strongly non-separable are deeply related to the specifics of the chosen pair of algorithms. This battle for safety must thus be balanced with a need for crypto-agility.

Conclusion

While the concat combiner offers a reasonably safe method for creating hybrid signatures, improvements in terms of non-separability can be made to reach state-of-the-art signature security. Nonetheless, for most use cases, the concatenation approach complemented with weak non-separability safeguards such as using dedicated keys specifically labelled for hybrid signatures, is sufficient for a secure transition.

It is also worth noting that hybridizing signatures may not be your most urgent priority. For applications where performance is less critical, you can already use the post-quantum and highly trusted hash-based signatures (like SLH-DSA). Although they are slower and more resource-intensive, they provide robust security today, making an immediate move to hybrid schemes unnecessary in those contexts.

In conclusion, theory is not enough; the security of an application lies in the details of its implementation. If you implement these new cryptographic primitives, we strongly encourage you to submit your work for an evaluation: Synacktiv will be more than happy to accompany you in this process.

• 1. https://people.csail.mit.edu/silvio/Selected%20Scientific%20Papers/Digi…
• 2. https://blog.cloudflare.com/the-tls-post-quantum-experiment/
• 3. https://eprint.iacr.org/2022/975.pdf
• 4. https://cyber.gouv.fr/sites/default/files/document/pqc-transition-in-fr…
• 5. https://eprint.iacr.org/2023/423.pdf
• 6. https://www.ietf.org/archive/id/draft-ietf-lamps-pq-composite-sigs-00.h…