Transition post-quantique : L’hybridation des signatures

NB : Article original en anglais ici

L’hybridation cryptographique est la stratégie de choix pour une transition sécurisée vers l’ère post-quantique. En combinant la robustesse éprouvée des algorithmes actuels et la résistance des nouveaux standards face à la menace quantique, elle garantit une protection optimale. Cependant, cette double assurance a un coût : une mise en œuvre plus complexe et un impact non négligeable sur les performances. Cet article explore les considérations techniques et les meilleures pratiques pour la mise en œuvre de signatures hybrides robustes.

Brefs rappels et définitions

Schéma de signature

Bien que le concept de signature numérique soit déjà connu, un rappel ne fait jamais de mal. Un algorithme de signature est un mécanisme cryptographique utilisé pour vérifier l’authenticité, l’intégrité et la non-répudiation des données. Il repose sur la cryptographie asymétrique, qui met en jeu une clé en deux parties : une partie privée utilisée pour la signature et une partie publique utilisée pour la vérification. Il se compose de trois algorithmes :

• KeyGen(), responsable de la génération d’une clé, composée d’une partie privée et d’une partie publique.
• Sign(Kpriv, m), qui prend en entrée une partie privée de clé et un message, et génère une signature pour ledit message.
• Verify(Kpub, m, sig), qui prend en entrée une partie publique de clé, un message et une signature, et vérifie si la signature correspond bien à ce message et à cette clé.

Un schéma de signature numérique est dit « sécurisé » lorsqu’il est calculatoirement difficile pour un attaquant de forger des signatures sans connaître la clé privée associée. Il existe différents modèles d’adversaire pour challenger cette hypothèse1, comme celui de l’Existential Unforgeability against Chosen Message Attack (EUF-CMA). Dans ce modèle, un adversaire a accès à un oracle capable de signer des messages arbitraires, et son objectif est de produire une signature pour un nouveau message qui n’a pas été signé préalablement par l’oracle. Un schéma est donc considéré comme sécurisé au sens de l’EUF-CMA si aucun adversaire “efficace” (i.e. qui effectue moins d’opérations que la robustesse théorique du schéma de signature) n’existe.

Combination et hybridation

En cryptographie, un combineur est un algorithme qui fusionne plusieurs algorithmes de même type (signature / échange de clés) en un seul, dans l’espoir de bénéficier de toutes les propriétés de sécurité des algorithmes individuels. Un combineur de signatures prend donc un certain nombre d’algorithmes de signature, et génère un nouveau schéma de signature qui les englobe tous et se veut au moins aussi robuste que chacun d’eux pris individuellement (du moins, c’est ce que l’on espère).

L’hybridation est un cas particulier de combinaison, où des algorithmes classiques sont associés à des algorithmes post-quantiques. L’objectif principal est de créer un schéma cryptographique plus résilient, sécurisé à la fois contre les ordinateurs classiques et quantiques. Cette approche est exigée par de nombreuses institutions comme l’ANSSI en France, en raison de l’incertitude relative concernant la sécurité des schémas post-quantiques, qui ont été à ce jour moins étudiés et éprouvés en conditions réelles.

Ce principe de précaution s’est d’ailleurs déjà avéré utile par le passé. En effet, en 2019, une expérience menée par Cloudflare sur la transition post-quantique2 a évalué la faisabilité de l’utilisation de mécanismes d’échange de clés post-quantiques dans le protocole TLS. Pour ce faire, Cloudflare s’est appuyé sur deux algorithmes post-quantiques, SIKE et NTRU-HRSS, tous deux hybridés avec l’algorithme classique X25519. Malheureusement, en 2022, W. Castryk et T. Decru ont découvert une attaque sur SIKE 3 qui a totalement anéanti les propriétés de sécurité de ce schéma, même face à un ordinateur classique. Si Cloudflare n’avait pas hybridé cet algorithme avec un algorithme classique robuste, les échanges de clés SIKE réalisés lors de cette expérience de 2019 seraient aujourd’hui trivialement cassés par un attaquant en position d’homme du milieu qui aurait enregistré les communications TLS de l’époque.

L’autre avantage d’une telle construction algorithmique générique est la crypto-agilité, c’est-à-dire la capacité à permettre d’interchanger de manière transparente les primitives cryptographiques. Cela aide à atténuer le point de défaillance unique que pourrait constituer une primitive cryptographique vulnérable utilisée seule.

Le domaine de la cryptographie post-quantique se concentrant actuellement principalement sur l’établissement de clés et les signatures numériques, nous nous focaliserons sur ces deux domaines dans cette série d’articles. Celui-ci se penche sur le sujet des signatures hybrides, tandis que le prochain sera consacré aux mécanismes d’encapsulation de clé (KEM).

Bien que les combineurs puissent en théorie être construits pour assembler n algorithmes, nous ne couvrirons que le cas (le plus courant) où n = 2. Plus spécifiquement, nous nous concentrerons sur le modèle hybride qui combine un unique algorithme classique avec un unique algorithme post-quantique.

Combiner des algorithmes de signature

Le combineur par concaténation

Une première intuition de construction permettant de combiner deux algorithmes de signature pourrait être : « Signons simplement le message avec les deux algorithmes, envoyons les deux signatures et vérifions-les toutes ». Un tel schéma est en effet au moins aussi sûr que chaque algorithme pris individuellement.

Disons qu’Alice envoie un message signé à Bob avec ce schéma combiné, composé des algorithmes X et Y, où au moins l’un d’eux (disons X) est EUF-CMA. Pour forger une signature d’un message m dans ce schéma combiné, un attaquant devrait forger une signature pour m avec l’algorithme X et une signature avec l’algorithme Y. Cependant, comme X est EUF-CMA, cette tâche serait infaisable pour l’attaquant. Ainsi, ce combineur de signatures est également sécurisé vis-à-vis de l’EUF-CMA. Plus généralement, casser une propriété de sécurité de ce combineur nécessite de la casser pour tous les algorithmes sous-jacents, ce qui garantit la propriété « au moins aussi sûr que chaque composant ».

À noter que ce combineur est la seule construction générique recommandée par l’ANSSI pour la combinaison de signatures dans sa présentation à Real-World PQC 20234.

Séparabilité

Bien que le schéma précédent soit intéressant dans un contexte entièrement hybride, un acteur malveillant pourrait extraire une unique signature (que ce soit celle de l’algorithme X ou Y) et l’utiliser seule, sans aucune preuve qu’elle faisait initialement partie d’une signature hybride, déviant ainsi de l’intention hybride originelle d’Alice. Cela pourrait se produire si le vérificateur accepte également les signatures avec seulement X ou Y en utilisant des parties de la clé hybride, pour des raisons de compatibilité par exemple. Cette propriété est appelée « séparabilité », et est discutée en détails dans un article de 2023 par N. Bindel et B. Hale 5.

Les chercheurs mettent en évidence deux niveaux de non-séparabilité : le premier, la non-séparabilité faible, où les signatures sont toujours réalisées indépendamment l’une de l’autre, et les « preuves d’hybridation » sont implémentées au niveau du protocole. Des exemples de telles preuves pourraient être :

• Utiliser la spécification draft de l’IETF sur les signatures composites6, qui revient globalement à utiliser le combineur par concaténation pour signer "HYBRIDSIG"||m
• Utiliser une clé dédiée, spécifiquement publiée pour les signatures hybrides (avec un attribut Key Usage spécifique dans le certificat par exemple)

Un second niveau de non-séparabilité (appelé non-séparabilité forte) est également présenté. Cette fois, les artéfacts sont implémentés au niveau de l’algorithme. Un exemple de schéma fortement non-séparable, adapté de l’article de N. Bindel et B. Hale pour des raisons de simplicité et combinant un schéma basé sur Fiat-Shamir (comme ML-DSA) avec RSA, est le suivant :

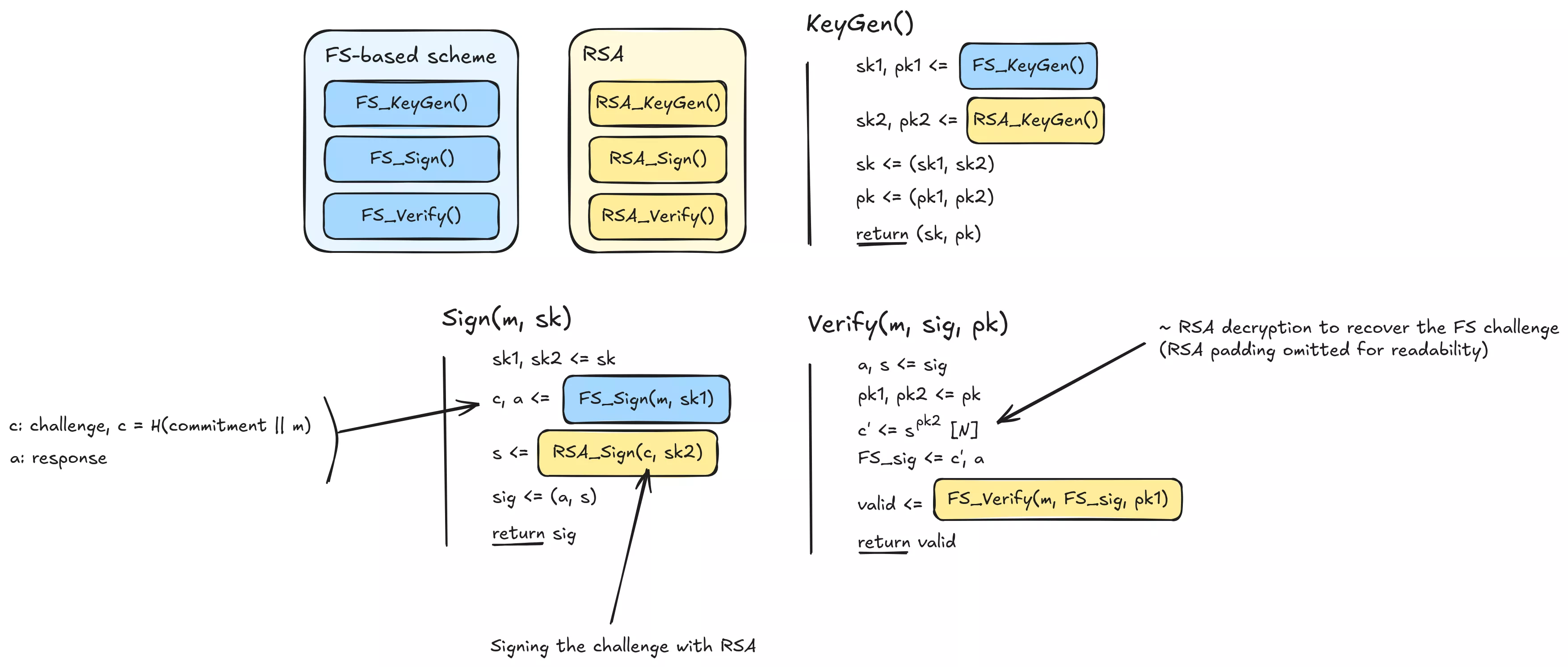
Ici, la signature RSA n’est pas directement liée au message et n’a pas de sens en elle-même, et la signature de Fiat-Shamir est incomplète sans les données RSA. Ce schéma est donc fortement non-séparable, car il est impossible de vérifier une signature composante sans impliquer l’autre algorithme. De plus, il reste « au moins aussi robuste » que les algorithmes de signature individuels. Pour plus de détails sur les schémas de ce type, l’article original est très intéressant et abordable.

En plus d’empêcher un attaquant d’isoler une sous-signature, la non-séparabilité forte peut également permettre d’éviter des erreurs d’implémentation. Imaginons par exemple le code suivant :

import threading

def verify_X(key, message, signature):
    global valid
    isXValid = True # placeholder pour la vérification de signature avec X
    valid &= isXValid

def verify_Y(key, message, signature):
    global valid
    isYValid = True # placeholder pour la vérification de signature avec Y
    valid &= isYValid

key = "aaa"
message = "bbb"
signature = "ccc"

# Variable globale "valid"
valid = True

thread_x = threading.Thread(target=verify_X, args=(key, message, signature))
thread_y = threading.Thread(target=verify_Y, args=(key, message, signature))

# Démarrage des threads de vérification
thread_x.start()
thread_y.start()
# Attente de la fin des deux threads
thread_x.join()
thread_y.join()

print(f"Hybrid signature validity is: {valid}")

Ce code semble correct à première vue (à l’exception d’une potentielle condition de concurrence, non pertinente ici), parallélisant la vérification des signatures pour de meilleures performances :

$ python3 hybrid_parallel.py 
Hybrid signature validity is: True

Cependant, imaginons que verify_Y lève une exception pour une raison quelconque :

def verify_Y(key, message, signature):
    global valid
    raise Exception() # crash during Y verification
    isYValid = False
    valid &= isYValid

Le code se comporterait alors de la sorte :

$ python3 hybrid_parallel.py 
Exception in thread Thread-2 (verify_Y):
Traceback (most recent call last):
  File "/usr/lib/python3.11/threading.py", line 1038, in _bootstrap_inner
    self.run()
  File "/usr/lib/python3.11/threading.py", line 975, in run
    self._target(*self._args, **self._kwargs)
  File "/tmp/hybrid_parallel.py", line 10, in verify_Y
    raise Exception()
Exception
Hybrid signature validity is: True

Bien qu’une exception soit levée dans le thread Y, elle n’est pas fatale pour le programme et la signature est considérée comme valide. Cela ne pourrait pas se produire avec un schéma hybride fortement non-séparable, où les signatures sont mathématiquement interdépendantes.

Cependant, la non-séparabilité forte s’accompagne d’un défi en matière de crypto-agilité. Le niveau d’intrication des deux algorithmes impliqués signifie que les routines de signature / vérification ne peuvent plus être traitées comme des boîtes noires fonctionnant en parallèle, et les ajustements nécessaires pour rendre une combinaison fortement non-séparable sont profondément liés aux spécificités de la paire d’algorithmes choisie. Cette bataille pour la sécurité doit donc être pondérée avec le besoin de crypto-agilité.

Conclusion

Bien que le combineur par concaténation offre une méthode raisonnablement sûre pour créer des signatures hybrides, des améliorations en termes de non-séparabilité peuvent être apportées pour atteindre l’état de l’art en matière de sécurité des signatures. Néanmoins, pour la plupart des cas d’usage, l’approche par concaténation, complétée par des protections de non-séparabilité faible telles que l’utilisation de clés dédiées et spécifiquement étiquetées pour les signatures hybrides, est suffisante pour une transition sécurisée.

Il est également à noter que l’hybridation des signatures n’est peut-être pas la priorité aujourd’hui, n’étant pas menacées tant qu’un ordinateur quantique suffisamment puissant n’existe pas. Si toutefois, pour une raison quelconque, l’envie de migrer dès aujourd’hui vous prenait, et pour des applications où la performance est moins critique, les schémas de signatures basées sur le hachage (comme SLH-DSA) sont déjà résistants face à la menace quantique. Bien qu’ils soient plus lents et plus gourmands en ressources, ces schémas offrent aujourd’hui une sécurité convenable et en laquelle le niveau de confiance est assez élevé, ce qui rend un passage par des schémas hybrides non nécessaire dans ces contextes.

En conclusion, la théorie ne suffit pas; la sécurité d’une implémentation réside dans ses détails. Si vous développez ces nouvelles primitives cryptographiques, nous vous encourageons vivement à soumettre votre travail pour une évaluation : Synacktiv se fera un plaisir de vous accompagner dans ce processus.

• 1. https://people.csail.mit.edu/silvio/Selected%20Scientific%20Papers/Digi…
• 2. https://blog.cloudflare.com/the-tls-post-quantum-experiment/
• 3. https://eprint.iacr.org/2022/975.pdf
• 4. https://cyber.gouv.fr/sites/default/files/document/pqc-transition-in-fr…
• 5. https://eprint.iacr.org/2023/423.pdf
• 6. https://www.ietf.org/archive/id/draft-ietf-lamps-pq-composite-sigs-00.h…